Uvedený studijní materiál se zabývá vlivem polů přenosu lineárního systému na jeho vlastnosti v kmitočtové a časové oblasti. Navazuje na kapitolu odezva.mws, zabývající se odezvou lineárního systému na harmonický signál. Pro pochopení této látky je potřebné znát Bodeho aproximaci kmitočtových charakteristik (modulové a fázové) přenosových funkcí. Přenosovou funkci  předpokládáme ve tvaru racionálně lomené funkce. Dále je třeba znát Laplaceovu transformaci a její použití při konstrukci impulzní a přechodové charakteristiky.  
restart: 

Pro výpočty a kreslení někrerých grafů budeme potřebovat tyto knihovny.  

>	with(plots):with(inttrans):with(plottools):

 

Póly přenosových funkcí 

Pro přenosy s jedním pólem předpokládejme přenosovou funkci systému v tomto taru. 

>	P:=K/(p-p1);

 

(1)

 

Jeden pól v levé polorovině 

Jeden pól v pravé polorovině 

Komplexně sdružená dvojice pólů 

Toto jsou samozřejmě oddělené jednoduché případy. Jsou to však všechny možné případy, které u reálných přenosů lineárních nebo linearizovaných soustav nastávají. Ve složitějších případech lze výraz pro modul přenosu rozdělit na součin takovýchto jednoduchých tvarů a jelikož modul je logaritmem absolutní hodnoty tohoto součinu, resp. logaritmem součinu jednotlivých absolutních hodnot, lze jejich známé vlastnosti jednoduše spojovat (sčítat). Podobně tomu je i pro fázi. Výsledná fáze je součtem fází jednotlivých částí přenosu (zde se násobí exponenciely fází, tj. exponenty = fáze se sčítají. "Sčítání platí i pro časové odezvy. Složitější výraz pro přenos, vyjádřený racionálně lomenou funkcí lze rozdělit na součet kořenových činitelů a na ty pak lze aplikovat výše uvedené metody.  

Nuly (a póly) přenosových funkcí 

U přenosových funkcí obsahujících nuly přenosu, je nutné si uvědimit jednu důležitou skutečnost. Přenosová funkce se totiž nemůže skládat pouze z jedné nebo více nul, ale vždy musí mít i odpovídající počet pólů přenosu, resp. je-li přenosová funkce ve tvaru racionálně lomenné funkce musí být být stupeň čitatele nižší než stupeň jmenovatele.   

Vysvětlení lze podat dvěma způsoby: 

• Přenosová funkce  jakéhokoliv reálného obvodu se bude jistě pro velmi vysoké kmitočty blížit nule, tj, provedeme-li substituci , musí platit . To bude však platit právě pro výše uvedenou vlastnost přenosu.

• Druhé vysvětlení je čistě matematické: Nutná a postačující podmínka pro to, aby racionální lomená funkce byla obrazem funkce sdandartního typu je, tato: Stupeň čitatele je nižší než stupeň jmenovatele. (Musí také platit První věta o limitě , kde je obraz předmětu standardního typu, resp. kdyby tato limita neplatila, nebude standardního typu). Důkaz této věty není předmětem našeho zájmu, tudíž se jím nebudem zabývat. Lze ho však nalézt např. v [LT], (viz také odezva.mws).

Pokusíme-li se přesto najít předmět např. funkce 1. Víme, že předmětem je Diracova funkce, tj. není funkce standardního typu (není to také reálný signál). 

>	invlaplace(1,p,t);

 

(2)

 

>	Int(Dirac(t),t = -infinity..infinity):%=value(%);

 

(3)

 

Obvodem, jež v ideálním případě nebude mít žádný pól kmitočtově závislého přenosu, může být např. derivátor. Ten je ukázán na následujícím obrázku. Jeho přenos je roven .    

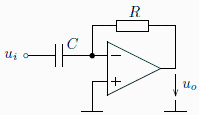
Inverzní Laplaceovu transformaci tohoto přenosu lze vyjádřit vztahem:   

>	invlaplace(p*tau,p,t);

 

(4)

 

Předmet k Laplaceovu obrazu obecného typu je vyjádřen následujícím výsledkem. 

>	invlaplace(K*(p-n0),p,t);

 

(5)

 

Zde je ukázáno, co je míněno zápisem . Je to zřejmě  derivace Diracovy funkce, což je opět nereálný signál.   

>	Diff(Heaviside(t),t):%=value(%);

 

>	Diff(Dirac(t),t):%=value(%);

 

>	Diff(Dirac(1,t),t):%=value(%);

 

 

 

	(6)

 

Je nutné si uvědomit, že v případě realizace výše uvedeného zapojení při použití reálného operačního zesilovače nedostaneme, vlivem  jeho kmitočtové závislosti, pro přenos uvedený vztah. V reálných podmínkách bude tedy vždy platit, že supeň čitatele je nižší než stupeň jmenovatale přenosu (pro velmi vysoký kmitočet se bude přenos blížit k nule - vlivem kmitočtové vávislosti zesílení, výstupní vnitřní impedanci a výstupní kapacitě). 

Věnujme se však ještě dalšímu idealizovanému případu, kdy je stupeň čitatele i jmenovatele přenosové funkce shodný a tudíž je přenos takovéhoto systému nenulový i pro , což nelze v praxi realizovat. Uvedený případ demonstrujme na přenosu, který obsahuje jednu nulu i pól  v levé polorovině komplexní roviny  . 

>	P:=K*(p-n1)/(p-p1);

 

(7)

 

Reálná pól i nula přenosu v levé polorovině 

>

 

Reálný pól v levé polorovině a nula přenosu v nule (pro nulový kmitočet) 

>

 

Reálná pól v levé polorovině a nula přenosu v pravé polorovině 

>

 

Následují příklady přenosů s komplexně sdruženou dvojicí pólů. Jsou ukázány vlastnosti přenosu obsahující jenu nebo dvě nuly přenosu, ležící na reálné ose i přenosu s komplexně sdruženou dvojicí nul.      

Komplexně sdružený pól a nuly přenosu na reálné ose 

Nyní již známe všechy možné případy, které se mohou vyskytnout v přenosech lineárních nebo linearizovaných soustav s jednoduchými i koplexně sdruženými póly a s jednoduchými nulami přenosu. Následují případy s komlexně sdruženou dvojicí nul přenosu. Jelikož nuly přenosu nemájí vliv na stabilitu obvodu, je situace daleko jednodužší než tomu bylo v případě pólů přenosu. Vliv na kmitočtové charakteristiky je u koplexně sdružených nul přesně inverzní (zrcadlově převrácený podle osy ) oproti koplexně sdruženým pólům, tudíž známý. Rozdíl je pouze v případě nul v pravé polorovině, kde modulová charakteristika zůstává inverzní, ale fázová chrakteristika je shodná jako v případě pólů. O příspěvcích jednotlivých pólů na celkové vlastnosti (v kmitočtové oblasti) jsme hovořili na závěr minulé kapitoly (aeo_pol.mws). Tyto poznatky samozřejmě platí i zde, pro přenosy obsahující jak póly tak nuly.  

Definujme přenos opět v následujícím tvaru, terý také upravíme pro zadání parametrů a , tj. s přenosem ve tvaru .  

>	P:=K*(p-n1)*(p-n2)/(p-p1)/(p-p2);

 

>	Pq:=numer(P)/expand(subs({p1=(-1+sqrt(1-4*Q^2))*omega[0]/2/Q,p2=(-1-sqrt(1-4*Q^2))*omega[0]/2/Q},denom(P)));

 

 

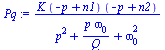	(8)

 

>

 

Komplexně sdružený pól i nula přenosu 

>