Jeden pól v levé polorovině
Např. pro 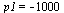 a
a 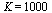 dostaneme
dostaneme
| > |
Pf:=unapply(abs(subs({K=1000,p1=-1000,p=sigma+I*omega},P)),(omega,sigma)); |
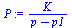 |
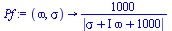 |
(1.1) |
| > |
complexplot([-1000],Re=-1100..1100,Im=-1.1..1.1,style=point,symbol=diamond,tickmarks=[1,1],title=`Umístění pólu p1`,labelfont=[HELVETICA],axesfont=[HELVETICA],symbolsize=25,symbol=diagonalcross); |
Takovýto přenos vykazuje například tento jednoduchý RC článek. (Pro ss. signál je 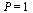 , proto
, proto 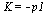 .)
.)
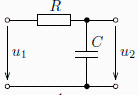
"Komplexní kmitočet" je ve tvaru 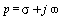 .
.
| > |
Surface:=plot3d(Pf,1..3000,-200..200,style=patchnogrid,axes=box,orientation=[-60,50]):
curve_o:=[omega,0,Pf(omega,0)]:
B_o:=spacecurve(curve_o,omega=1..3000,axes=none,color=black,thickness=3):
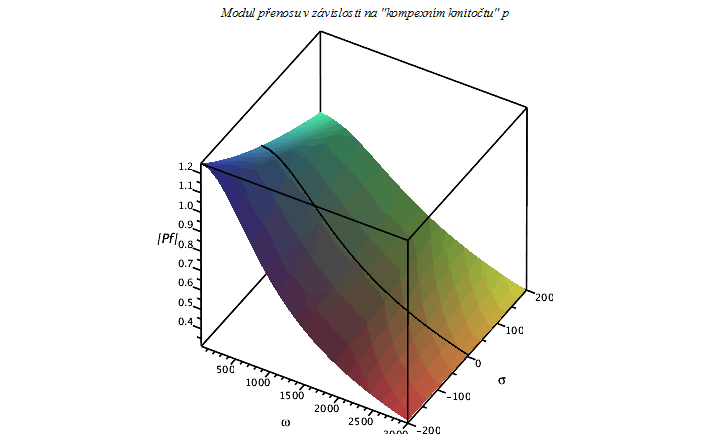
display(Surface,B_o,labels=[omega,sigma,`|Pf|`],title=`Modul přenosu v závislosti na "kompexním kmitočtu" p`,labelfont=[HELVETICA],axesfont=[HELVETICA,8]); |
Je zřejmé, že pro klesající 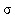 vzrůstá přenos (pro
vzrůstá přenos (pro 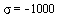 a
a 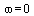 vykazuje přenos maximum (
vykazuje přenos maximum (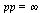 )), jak je také vidět na následujícím grafu.
)), jak je také vidět na následujícím grafu.
| > |
plot3d(Pf,1..3000,-2000..200,style=patch,axes=box,orientation=[-60,50],labels=[omega,sigma,`|Pf|`],title=`Modul přenosu v závislosti na "kompexním kmitočtu" p`,labelfont=[HELVETICA],axesfont=[HELVETICA,8]); |
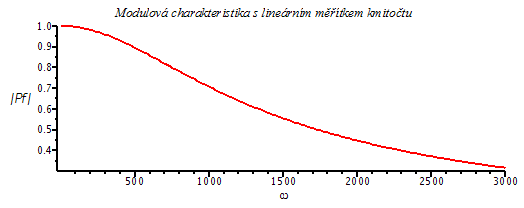
Jestliže nyní vykreslíme průmět tohoto 3D grafu pro 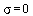 (na prvním grafu označeno černou křivkou) , dostaneme známou modulovou chrakteristiku (
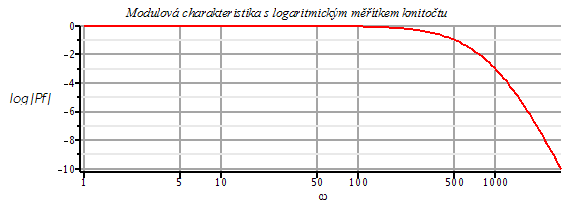
(na prvním grafu označeno černou křivkou) , dostaneme známou modulovou chrakteristiku (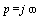 ). Na následujících průbězích je navíc ukázáno srovnání pro lineární a logaritmickou stupnici úhlového kmitočtu w (3D grafy mají lineární měřítka). Zlomovým kmitočtem (kmitočtem, při němž modul přenosu poklesne o 3dB) je zde přímo hodnota pólu přenosové funkce.
). Na následujících průbězích je navíc ukázáno srovnání pro lineární a logaritmickou stupnici úhlového kmitočtu w (3D grafy mají lineární měřítka). Zlomovým kmitočtem (kmitočtem, při němž modul přenosu poklesne o 3dB) je zde přímo hodnota pólu přenosové funkce.
| > |
plot(Pf(omega,0),omega=1..3000,title=`Modulová charakteristika s lineárním měřítkem kmitočtu`,labels=[omega,`|Pf|`],labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2);
semilogplot(20*log10(Pf(omega,0)),omega=1..3000,y=-10..0,title=`Modulová charakteristika s logaritmickým měřítkem kmitočtu`,labels=[omega,`log|Pf|`],axes=FRAME,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2,gridlines=true); |
Jestliže provedeme inverzní Laplaceovu transformaci výrazu pro přenos, dostaneme rovnici pro příslušnou impulzní charakteristiku (odezvu na Dirakúv pulz), případně i přechodovou charalteristiku (odezvu na jednotkový skok).
| > |
Pt:=invlaplace(P, p, t); |
| > |
Ptp:=invlaplace(P/p, p, t); |
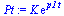 |
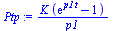 |
(1.2) |
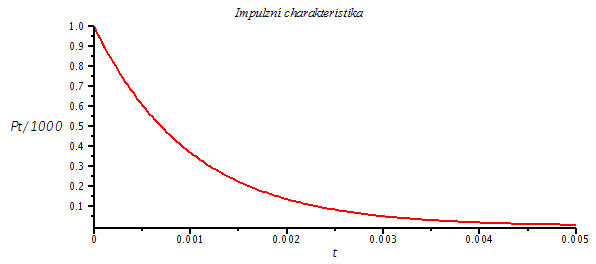
Pro stabilní systém je nutné, aby po odeznění přechodovédo děje se výstupní veličina lineárního systému ustálila na konečné hodnotě. To znamená, že pól p1 musí být záporný, jak tomu je v tomto příkladě a což dokazuje následující výpočet i graf.
| > |
`Pt `(t=infinity)=limit(Pt,t=infinity) assuming (p1<0);
plot(subs({K=1000,p1=-1000},Pt/1000),t=0..0.005,labels=[t,`Pt/1000`],title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
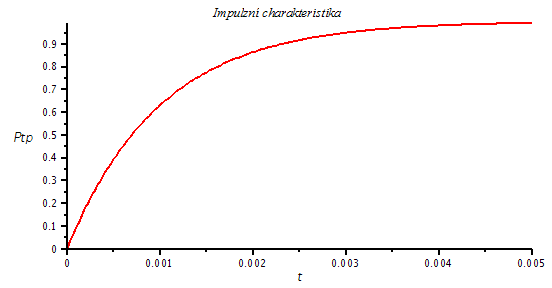
Pro úplnost je uvedena odezva na jedtkový impulz.
| > |
`Ptp `(t=infinity)=limit(Ptp,t=infinity) assuming (p1<0);
plot(subs({K=1000,p1=-1000},Ptp),t=0..0.005,labels=[t,` Ptp`],title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
![]() a
a ![]() dostaneme
dostaneme 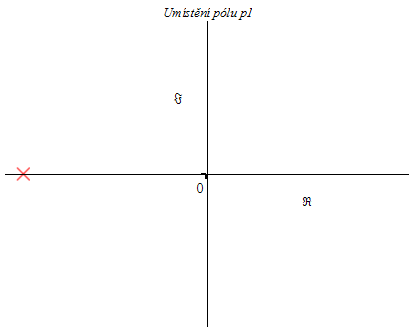
![]() , proto
, proto ![]() .)
.)

![]() .
. 
![]() vzrůstá přenos (pro
vzrůstá přenos (pro ![]() a
a ![]() vykazuje přenos maximum (
vykazuje přenos maximum (![]() )), jak je také vidět na následujícím grafu.
)), jak je také vidět na následujícím grafu. 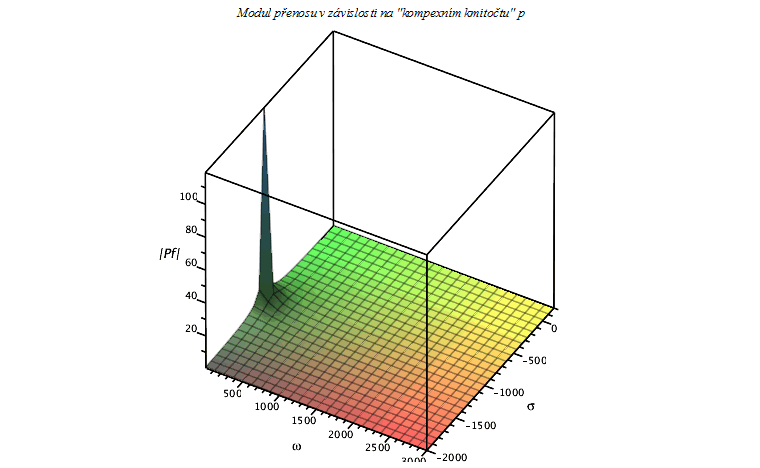
![]() (na prvním grafu označeno černou křivkou) , dostaneme známou modulovou chrakteristiku (
(na prvním grafu označeno černou křivkou) , dostaneme známou modulovou chrakteristiku (![]() ). Na následujících průbězích je navíc ukázáno srovnání pro lineární a logaritmickou stupnici úhlového kmitočtu w (3D grafy mají lineární měřítka). Zlomovým kmitočtem (kmitočtem, při němž modul přenosu poklesne o 3dB) je zde přímo hodnota pólu přenosové funkce.
). Na následujících průbězích je navíc ukázáno srovnání pro lineární a logaritmickou stupnici úhlového kmitočtu w (3D grafy mají lineární měřítka). Zlomovým kmitočtem (kmitočtem, při němž modul přenosu poklesne o 3dB) je zde přímo hodnota pólu přenosové funkce.