Základní vztahy
Základní perioda signálu
| > | ![T = 1/f[0]](images_fr/fr1.gif)
|
Základní úhlová frekvence
| > |
Goniometrický tvar
| > | ![f(t) = a[0]+Sum(a[k]*cos(k*omega[0]*t)+b[k]*sin(k*omega[0]*t),k = 1 .. infinity)](images_fr/fr3.gif)
|
| > | ![a[0] = ('1/T')*int(f(t),t = 0 .. T)](images_fr/fr4.gif)
|
| > | ![a[k] = ('2/T')*Int(f(t)*cos(k*omega[0]*t),t = 0 .. T)](images_fr/fr5.gif)
|
| > | ![b[k] = ('2/T')*Int(f(t)*sin(k*omega[0]*t),t = 0 .. T)](images_fr/fr6.gif)
|
Amplitudový tvar
| > | ![f(t) = B[0]+Sum(Bm[k]*sin(k*omega[0]*t+phi[k]),k = 1 .. infinity)](images_fr/fr7.gif)
|
| > |
| > |
| > | ![tan(phi[k]) = a[k]/b[k]; phi[k] = arctan(a[k],b[k])](images_fr/fr10.gif)
|
Exponenciální tvar
| > | ![f(t) = Sum(c[k]*exp(j*k*omega[0]*t),k = -infinity .. infinity)](images_fr/fr11.gif)
|
| > | ![c[k] = ('1/T')*Int(f(t)*exp(-j*k*omega[0]*t),t = 0 .. T)](images_fr/fr12.gif)
|
| > |
| > | ![c[k] = (a[k]-j*b[k])/2](images_fr/fr14.gif)
|
Určov
ání koeficientů Fourierovy řady
© Jiří Hospodka
Následující ukázka demonstroje použití programu Maple při podpoře výuky Fourierových řad v předmětech Elektrické obvody 2 (EO2) a počítačové řešení elektrických obvodů (PRO).
| > |
Základní vztahy
Základní perioda signálu
| > | ![T = 1/f[0]](images_fr/fr1.gif)
|
Základní úhlová frekvence
| > |
Goniometrický tvar
| > | ![f(t) = a[0]+Sum(a[k]*cos(k*omega[0]*t)+b[k]*sin(k*omega[0]*t),k = 1 .. infinity)](images_fr/fr3.gif)
|
| > | ![a[0] = ('1/T')*int(f(t),t = 0 .. T)](images_fr/fr4.gif)
|
| > | ![a[k] = ('2/T')*Int(f(t)*cos(k*omega[0]*t),t = 0 .. T)](images_fr/fr5.gif)
|
| > | ![b[k] = ('2/T')*Int(f(t)*sin(k*omega[0]*t),t = 0 .. T)](images_fr/fr6.gif)
|
Amplitudový tvar
| > | ![f(t) = B[0]+Sum(Bm[k]*sin(k*omega[0]*t+phi[k]),k = 1 .. infinity)](images_fr/fr7.gif)
|
| > |
| > |
| > | ![tan(phi[k]) = a[k]/b[k]; phi[k] = arctan(a[k],b[k])](images_fr/fr10.gif)
|
Exponenciální tvar
| > | ![f(t) = Sum(c[k]*exp(j*k*omega[0]*t),k = -infinity .. infinity)](images_fr/fr11.gif)
|
| > | ![c[k] = ('1/T')*Int(f(t)*exp(-j*k*omega[0]*t),t = 0 .. T)](images_fr/fr12.gif)
|
| > |
| > | ![c[k] = (a[k]-j*b[k])/2](images_fr/fr14.gif)
|
| > |
Obdélníkový průběh posunutý o
![]()
Definice výrazu pro obdélníkový průběh, posunutý o
![]() a jeho vykreslení.
a jeho vykreslení.
| > | v_obd:=signum(cos(2*Pi*t)); |
| > | prubeh_obd:=plot(v_obd,t=0..1.5,color=blue):prubeh_obd; |
![]()
![[Maple Plot]](images_fr/fr18.gif)
Definice funkce signum
| > | convert(signum(x),piecewise); |
![PIECEWISE([-1, x < 0],[0, x = 0],[1, 0 < x])](images_fr/fr19.gif)
Nejprve určíme obecné vztahy pro oba koeficienty. Je zřejmé, že výsledná řada nebude obsahovat sinové složky.
| > | a_obd:=8/T*int(1*cos(k*2*Pi/T*t), t=0..T/4 ); |
| > | b_obd:=4/T*int(1*sin(k*2*Pi/T*t), t=-T/4..T/4 ); |
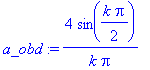
![]()
Vypsání prvních deseti koeficientů. Je evidentní, že pro sudé násobky základní harmonické jsou koeficienty nulové.
| > | a_obd_k:=seq(eval(a_obd),k=1..10); |
![]()
Vykreslení velikostí (absolutních hodnot) prvních dvaceti harmonických - ze zvyšující se harmonickou klesá amplituda jen "pozvolna".
| > | p1:=plot([[[0,0],[0,0]],seq([[k,0],[k,abs(a_obd)]],k=1..20)],color=black,thickness=3,xtickmarks=20): |
| > | p1; |
![[Maple Plot]](images_fr/fr23.gif)
Vyjádření Fouryerovy řady uvedeného průběhu pomocí funkce
![]() , její vyčíslení pro prvních deset harmonických (pět nenulových) a vykreslení.
, její vyčíslení pro prvních deset harmonických (pět nenulových) a vykreslení.
| > | f_obd:=(t,n)->sum(a_obd*cos(2*Pi*k*t),k=1..n); |
| > | temp:=f_obd(t,10); |
| > | plot(temp,t=0..1.5,thickness=2); |
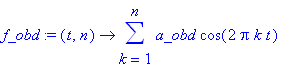
![]()
![[Maple Plot]](images_fr/fr27.gif)
Vykreslení výsledného průběhu pro různý počet harmonických i pomocí animace.
| > | plots[animate](plot,[f_obd(t,i),t=0..1.5,numpoints=500,thickness=2],i=[5,10,15,20,30,50,100],background=prubeh_obd); |
![[Maple Plot]](images_fr/fr28.gif)
| > | f_obd:=(t,n)->sum(a_obd*cos(2*Pi*k*t),k=1..n); |
| > | temp:=f_obd(t,10); |
| > | plot(temp,t=0..1.5,thickness=2); |
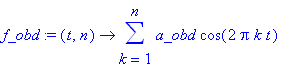
![]()
Ostatní typy Fourierových řad
Amplitudový tvar je v tomto případě parakticky shodný s výše uvedeným goniometrickým vztahem (
![]() ,
,
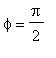 ), jelikož je evidentní, že
), jelikož je evidentní, že
| > | simplify(sin(x+Pi/2)); |
![]()
V případě exponenciálního tvaru vypočteme příslušný integrál - za fumkci nyní dosadíme přímo výše uvedený výraz.
| > | ck_obd:=1/1*int(v_obd*exp(-I*k*2*Pi/1*t), t=0..1);# assuming k::posint; |
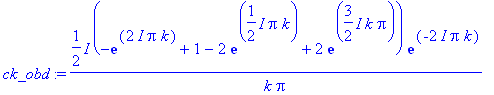
Výsledek je shodný (součet je zapsán pouze v opačném poředí) - není třeba znovu vykreslovat.
| > | f_obd:=(t,n)->sum(ck_obd*exp(I*2*Pi*k*t),k=-n..-1)+sum(ck_obd*exp(I*2*Pi*k*t),k=1..n); |
| > | temp:=evalc(f_obd(t,10)); |
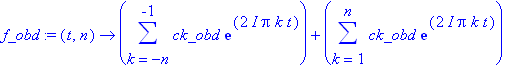
![]()
Dále následuje výpočet pro další průběhy již s minimálním komentářem (viz. také nápovědu uvedených příkazů programu Maple). Pro jednoduchost bude výpočet proveden pouze pro goniometrický tvar Fourierovy řady.
Jednocestně usměrněný sinusový průběh
| > | prubeh_s1:=plot((signum(sin(2*Pi*t))/2+1/2)*sin(2*Pi*t),t=0..1.5,color=blue): |
| > | prubeh_s1; |
![[Maple Plot]](images_fr/fr37.gif)
| > | b_s1:=2/T*int(1*sin(2*Pi/T*t)*sin(k*2*Pi/T*t), t=0..T/2); |
| > | a_s1:=2/T*int(1*sin(2*Pi/T*t)*cos(k*2*Pi/T*t), t=0..T/2); |
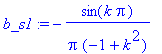
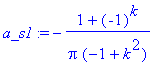
Lze i s předpokladem, ale ...
Lze i takto, ale ne vždy dostaneme správný výsledek (tak kde se musí počítat limita).
| > | 2/T*int(1*sin(2*Pi/T*t)*sin(k*2*Pi/T*t), t=0..T/2) assuming k::posint; |
| > | 2/T*int(1*sin(2*Pi/T*t)*cos(k*2*Pi/T*t), t=0..T/2) assuming k::posint; |
![]()
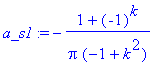
| > | a0_s1:=limit(a_s1,k=0); |
Pro případ
![]() je nutné počítat limitu, protože jinak vyjde dělení nulou.
je nutné počítat limitu, protože jinak vyjde dělení nulou.
| > | limit(a_s1,k=1); |
| > | limit(b_s1,k=1); |
![]()
![]()
![]()
| > | seq(eval(a_s1),k=2..5); |
| > | seq(eval(b_s1),k=2..5); |
![]()
![]()
| > | plots[animate](plot,[a0_s1/2+1/2*sin(2*Pi*t)+sum(a_s1*cos(k*2*Pi*t),k=2..i),t=0..1.5,numpoints=100,thickness=2],i=[3,5,10,20,50],background=prubeh_s1); |
![[Maple Plot]](images_fr/fr48.gif)
| > |
Dvojcestně usměrněný sinusový průběh
| > | prubeh_s2:=plot(abs(sin(2*Pi*t)),t=0..1.5,color=blue): |
| > | prubeh_s2; |
![[Maple Plot]](images_fr/fr49.gif)
| > | a_s2:=4/T*int(1*sin(2*Pi/T*t)*cos(k*2*Pi/T*t), t=0..T/2); |
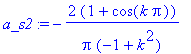
| > | a0_s2:=limit(a_s2,k=0); |
Pro případ
![]() je nutné počítat limitu, protože jinak vyjde dělení nulou.
je nutné počítat limitu, protože jinak vyjde dělení nulou.
| > | limit(a_s2,k=1); |
![]()
![]()
| > | seq(eval(a_s2),k=2..5); |
![]()
| > | plots[animate](plot,[a0_s2/2+sum(a_s2*cos(k*2*Pi*t),k=2..i),t=0..1.5,numpoints=100,thickness=2],i=[3,5,10,20,50],background=prubeh_s2); |
![[Maple Plot]](images_fr/fr55.gif)
Spektrální čáry (koeficienty) se zmenšují směrem k vyšším harmonickým daleko výrazněji, než tomu bylo pro obdélníkový průběh, který obsahuje nekonečně strmé přechody (hrany), které jsou právě příčinou vzniku nezanedbatelně velkých vyšších harmonických. Pokud porovnáme vztahy pro oba koeficienty, zjistíme, že vztah pro koeficienty obdélníkového průběhu obsahuje činitek
![]() (jednotlivé koeficienty se násobí výrazem
(jednotlivé koeficienty se násobí výrazem
![]() ), naproti tomu výraz pro koeficienty tohoto průběhu obsahuje činitel
), naproti tomu výraz pro koeficienty tohoto průběhu obsahuje činitel
![]() , proto se tyto koeficienty zmenšují s rostoucí harmonickou (
, proto se tyto koeficienty zmenšují s rostoucí harmonickou (
![]() ) mnohem výrazněji.
) mnohem výrazněji.
| > | p2:=plot([[[0,0],[0,a0_s2]],seq([[k,0],[k,abs(a_s2)]],k=2..20)],color=red,thickness=3,xtickmarks=20): |
| > | plots[display](p1,p2); |
![[Maple Plot]](images_fr/fr60.gif)
| > |
Trojůhelníkový průběh
Takto jednoduše lze definovat trojůhelníkový průběh.
| > | troj:=(4*(t-floor(t+1/4))-1)*signum(cos(2*Pi*t))+1; |
![]()
| > |
Průběh funkce floor
| > | plot(floor(t),t=-0.5..2.5,thickness=2); |
![[Maple Plot]](images_fr/fr62.gif)
Zde je vykreslen výše definovaný průběh spolu s první a druhou harmonickou.
| > | prubeh_troj:=plot(troj,t=0..1.5,color=blue): |
| > | sin12:=plot([sin(2*Pi*t),0.5*sin(4*Pi*t)],t=0..1.5,color=[green,red]): |
| > | plots[display](prubeh_troj,sin12); |
![[Maple Plot]](images_fr/fr63.gif)
Takto definovaný vztah je špatně - takto ne!, viz. výše uvedený obrázek průběhů trojůhelníkového spolu s první a druhou harmonickou.
| > | b_troj:=8/T*int(t*4/T*sin(k*2*Pi/T*t), t=0..T/4 ); |
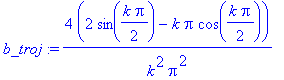
Je evidentní, že výsledné spektrum obsahuje i sudé harmonické, které musí vyjít nulové.
| > | bk:=seq(eval(b_troj),k=1..10); |
| > | bk:=seq(`if`(is(k,odd),eval(b_troj),0),k=1..10); |
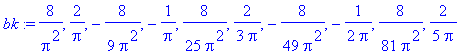
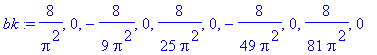
Je nutné počítat minimálně do poloviny periody - to však přináší komplikace - je nutné rozdělit integrál na dvě části (neumíme vyjádřit průběh jednou funkcí).
| > | b_troj:=simplify(4/T*int(t*4/T*sin(k*2*Pi/T*t),t=0..T/4)+4/T*int((2-t*4/T)*sin(k*2*Pi/T*t),t=T/4..T/2)); |
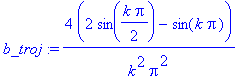
Výpis velikostí prvních deseti harmonických nyní ukazuje, že výpočet byl proveden správně.
| > | bk:=seq(eval(b_troj),k=1..10); |
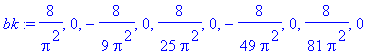
Maple samozřejmě dokáže pracovat i s výše definovaným průběhem troj , v našem případě integrovat. Pro vvyjádření koeficientu nyní využijme funkce (narozdíl od dříve používaných výrazů).
| > | b_troj:=unapply(simplify(4/1*int(troj*sin(k*2*Pi/1*t), t=0..1/2 )),k); |
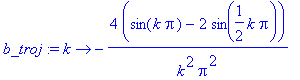
Vyjádření Fouryerovy řady uvedeného průběhu opět pomocí funkce
![]() .
.
| > | f_troj:=(t,n)->sum(b_troj(k)*sin(2*Pi*k*t),k=1..n); |
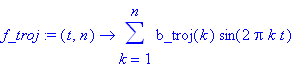
Tady je výsledná animace.
| > | plots[animate](plot,[f_troj(t,i),t=0..1.5,numpoints=100,thickness=2],i=[3,5,10,20,50],background=prubeh_troj); |
![[Maple Plot]](images_fr/fr72.gif)
Opět se spektrální čáry (koeficienty) tohoto průběhu zmenšují směrem k vyšším harmonickým daleko výrazněji, než tomu bylo pro obdélníkový průběh. Pro rozlišení jsou tyto čáry nepatrně posunuty vůči původním čarám, odpovídajícím obdélníkovému průběhu.
| > | p2:=plot([seq([[k+0.1,0],[k+0.1,abs(b_troj(k))]],k=1..20)],color=red,thickness=3,xtickmarks=20): |
| > | plots[display](p1,p2); |
![[Maple Plot]](images_fr/fr73.gif)
| > |
Pilový průběh
Takto jednoduše lze definovat trojůhelníkový průběh.
| > | pila:=t-floor(t); |
![]()
Zde je vykreslen výše definovaný průběh spolu s první a druhou harmonickou.
| > | prubeh_pila:=plot(pila,t=0..1.5,color=blue): |
| > | sin12:=plot([sin(2*Pi*t),0.5*sin(4*Pi*t)],t=0..1.5,color=[green,red]): |
| > | plots[display](prubeh_pila,sin12); |
![[Maple Plot]](images_fr/fr75.gif)
Výpočet koeficientů. Zde budou evidentně nenulové jak sudé, tak liché koeficienty sinnusové řady. Při výpočtu předpokládáme, že koeficient
![]() je přirozené číslo (positive integer), což zjednodušší výsledek, ale zároveň nedostaneme správnou hodnotu pro koeficient
je přirozené číslo (positive integer), což zjednodušší výsledek, ale zároveň nedostaneme správnou hodnotu pro koeficient
![]() , který je nutné počítat limitou (ostatní koecicienty jsou správně nulové).
, který je nutné počítat limitou (ostatní koecicienty jsou správně nulové).
| > | b_pila:=unapply(2/1*int(pila*sin(k*2*Pi/1*t),t=0..1),k) assuming k::posint; |
| > | a_pila:=unapply(2/1*int(pila*cos(k*2*Pi/1*t),t=0..1),k) assuming k::posint; |
![]()
![]()
Výpočet koeficientů
![]() bez uvažovaného předpokladu a vyčíslení koeficientu
bez uvažovaného předpokladu a vyčíslení koeficientu
![]() . To je nutné provést limitou (pro pouhé dosazení dostaneme chybové hlášení - dělení nulou) nebo přímým výpočtem integrálu.
. To je nutné provést limitou (pro pouhé dosazení dostaneme chybové hlášení - dělení nulou) nebo přímým výpočtem integrálu.
| > | a_p:=unapply(2/1*int(pila*cos(k*2*Pi/1*t),t=0..1),k); |
| > | a_p(0); |
| > | limit(a_p(x),x=0)/2; |
| > | a0:=int(pila,t=0..1); |
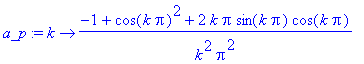
Error, (in a_p) numeric exception: division by zero
![]()
![]()
Následuje výpis prvních pěti koeficientů a vyjádření Fouryerovy řady uvedeného průběhu opět pomocí funkce
![]() .
.
| > | seq(b_pila(i),i=1..5); |
| > | f_pila:=(t,n)->a0+sum(b_pila(k)*sin(2*Pi*k*t),k=1..n); |
![]()
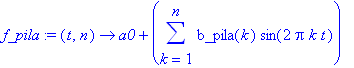
Zde je výsledná animace.
| > | plots[animate](plot,[f_pila(t,i),t=0..1.5,numpoints=200,thickness=2],i=[3,5,10,20,50,100],background=prubeh_pila); |
![[Maple Plot]](images_fr/fr88.gif)
V tomto případě se spektrální čáry (koeficienty) tohoto průběhu zmenšují směrem k vyšším harmonickým podobně jako tomu bylo v případě obdélníkového průběhu. Je to dáno nekonečně strmými hranami, jako v případě smíněného obdélníkového průběhu. Z tohoto důvodu figuruje ve jmenovateli vztahu pro koeficienty opět člen
![]() oproti členu
oproti členu
![]() , vyskytujícímu se u ostatních, zde uvedených, průběhů. Proto byl pokles velikostí jejich koeficientů řady daleko výraznější směrek k vyšším harmonickým. Navíc jsou v tomto případě přítomny jak sudé, tak liché harmonické, což je důsledek toho, že jsou koeficienty tohoto průběhu celkově menší, oproti koeficientům obdélníkového průběhu. Pro rozlišení jsou čáry lichých harmonických nepatrně posunuty vůči původním čarám, odpovídajícím obdélníkovému průběhu.
, vyskytujícímu se u ostatních, zde uvedených, průběhů. Proto byl pokles velikostí jejich koeficientů řady daleko výraznější směrek k vyšším harmonickým. Navíc jsou v tomto případě přítomny jak sudé, tak liché harmonické, což je důsledek toho, že jsou koeficienty tohoto průběhu celkově menší, oproti koeficientům obdélníkového průběhu. Pro rozlišení jsou čáry lichých harmonických nepatrně posunuty vůči původním čarám, odpovídajícím obdélníkovému průběhu.
| > | p2:=plot([[[0,0],[0,a0]],seq([[k+`if`(is(k,odd),0.1,0),0],[k+`if`(is(k,odd),0.1,0),abs(b_pila(k))]],k=1..20)],color=red,thickness=3,xtickmarks=20): |
| > | plots[display](p1,p2); |
![[Maple Plot]](images_fr/fr91.gif)
| > |
| > |
Něco navíc pro Maple
Kdo má program Maple nainstalovaný, může si vyzkoušrt tuto aplikaci pro výuku integrálů.
| > | with(Student[Calculus1]): |
| > | IntTutor(); |
Initializing Java runtime environment.
![]()
| > |