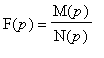 . Tato funkce má tzv. nulové body
. Tato funkce má tzv. nulové body
Odezva lineárního obvodu na harmonický signál
Tato kapitola se zabývá se odezvou lineárního systému na harmonický signál. Pro pochopení této látky je potřebné znát Laplaceovu transformaci a její použití v elektronických obvodech při konstrukci časových odezev speciálně pak pro impulzní a přechodové charakteristiky. Na závěr tohoto výkladu se však zmíníme o specifikách Laplaceovy a také Fourierovy transformace.
Tento soubor výkladů také předpokládá znalost alespoň základních příkazů Maple V (viz.
uvod.mws,
maple_in.mws a
syrup_in.mws).
restart:
Pro výpočty a kreslení někrerých grafů budeme potřebovat tyto knihovny.
| > | with(inttrans): |
Budeme uvažovat lineární, časově invariantní systém (bez paměti), který je popsán přenosovou funkcí ve tvaru racionálně lomené funkce
 . Tato funkce má tzv. nulové body
. Tato funkce má tzv. nulové body
![]() , jestliže platí
, jestliže platí
![]() . Funkce
. Funkce
![]() má dále póly
má dále póly
![]() , pokud
, pokud
![]() . Předpokládejme také, že přenosová funkce obvodu
. Předpokládejme také, že přenosová funkce obvodu
![]() je racionálně lomenou funkcí stupně
je racionálně lomenou funkcí stupně
![]() a platí
a platí
![]() . Obraz odezvy na signál s Laplaceovým obrazem
. Obraz odezvy na signál s Laplaceovým obrazem
![]() je dána výrazem
je dána výrazem
![]() . Odezvu o(t) dostaneme zpětnou LT a lze ji rozložit na
přirozenou (vlastní)
a
vynucenou složku
. Odezvu o(t) dostaneme zpětnou LT a lze ji rozložit na
přirozenou (vlastní)
a
vynucenou složku
![]() . Pro nalezení předmětu LT můžme s výhodou použít větu o reziduích ([LT], str.137 a [MA III] str.175), potom je
. Pro nalezení předmětu LT můžme s výhodou použít větu o reziduích ([LT], str.137 a [MA III] str.175), potom je
 = Sum(res[p[k]](O(p)*exp(p*t)),k)](images_odezva/odezva13.gif) a
a
 = Sum(res[p[j]](O(p)*exp(p*t)),j)](images_odezva/odezva14.gif) ,
,
kde
![]() jsou singulární body (póly) přenosové funkce
jsou singulární body (póly) přenosové funkce
![]() a
a
![]() jsou singulární body (póly) funkce
jsou singulární body (póly) funkce
![]() . Z tohoto vyplývá, že
je-li obvod
absolutně stabilní
, pak po připojení zdroje signálu k obvodu přirozená složka odezvy obvodu postopně zaniká
. Z tohoto vyplývá, že
je-li obvod
absolutně stabilní
, pak po připojení zdroje signálu k obvodu přirozená složka odezvy obvodu postopně zaniká
![]() , tudíž všechny póly přenosové funkce absolutně stabilního obvodu musí ležet v levé polorovině
, jak bude patrné z dalšího výkladu (
Jak se počítá residuum) a což bude také zřejmé z
aeo_pol.mws. Zanikající přirozená složka odezvy se přitom nazývá
přechodovou složkou
. Po zániku přechodové složky je odezva tvořena pouze vynucenou složkou a naopkak po odpojení budícího signálu je odezvva tvořena pouze přechodovou složkou. Při připojení zdroje signálu k obvodu v okamžiku
, tudíž všechny póly přenosové funkce absolutně stabilního obvodu musí ležet v levé polorovině
, jak bude patrné z dalšího výkladu (
Jak se počítá residuum) a což bude také zřejmé z
aeo_pol.mws. Zanikající přirozená složka odezvy se přitom nazývá
přechodovou složkou
. Po zániku přechodové složky je odezva tvořena pouze vynucenou složkou a naopkak po odpojení budícího signálu je odezvva tvořena pouze přechodovou složkou. Při připojení zdroje signálu k obvodu v okamžiku
![]() , pak pro počáteční a konečnou hodnotu odezvy platí podle vět o limitě:
, pak pro počáteční a konečnou hodnotu odezvy platí podle vět o limitě:
![]() a
a
![]() , (o(0+), p=>0+).
, (o(0+), p=>0+).
Připomeňme ještě dva často používané typy budení. Je-li budícím signálem Dirakův impulz (
![]() ), pak odezva obvodu na tento signál je funkce
), pak odezva obvodu na tento signál je funkce
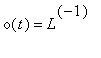
![]() , která se nazývá
impulzní charakteristika
obvodové funkce
, která se nazývá
impulzní charakteristika
obvodové funkce
![]() . Je-li dále budící signál ve tvaru jednotkového skoku (
. Je-li dále budící signál ve tvaru jednotkového skoku (
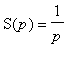 ), pak odezva obvodu na tento signál je
), pak odezva obvodu na tento signál je

 a nazývá se
přechodová charakteristika
obvodové funkce
a nazývá se
přechodová charakteristika
obvodové funkce
![]() . Její vztah k impulzní charakteristice je dán zmíněným integrálem. Z výše uvedeného lze ještě napsat počáteční a konečnou hodnotu přechodové charakteristiky:
. Její vztah k impulzní charakteristice je dán zmíněným integrálem. Z výše uvedeného lze ještě napsat počáteční a konečnou hodnotu přechodové charakteristiky:
![]() , resp.
, resp.
![]() a (pch(0+), p=>0+, F(0+))
a (pch(0+), p=>0+, F(0+))
![]() . , resp.
. , resp.
![]() , z čehož je patrné, že stupeň čitatele funkce
, z čehož je patrné, že stupeň čitatele funkce
![]() musí být nenší než stupeň jmenovatele --
musí být nenší než stupeň jmenovatele --
![]() , což platí u každého reálného obvodu (viz
aeo_nul.mws).
, což platí u každého reálného obvodu (viz
aeo_nul.mws).
Nyní odvodíme odezvu obdodu s výše definovanou přenosovou funkcí
![]() na obecný harmonický signál.
na obecný harmonický signál.
| > | vstup:=A*sin(omega*t+Phi); |
![]()
Obraz funkce
![]() .
.
| > | S:=laplace(vstup,t,p); |

Poznámka k Laplaceovu obrazu funkce
![]()
V některých pramenech se můžeme setkat s jiným vyjádřením obrazu funkce
![]() . Je to periodická funkce, tj. funkce, která není nulová pro záporný argument, proto ji při hledání Laplaceova obrazu násobíme jednotkovým skokem. Maple ji imlicitně násobí skokem v
. Je to periodická funkce, tj. funkce, která není nulová pro záporný argument, proto ji při hledání Laplaceova obrazu násobíme jednotkovým skokem. Maple ji imlicitně násobí skokem v
![]() (
(
![]() ). Při použití posunutého jednotkového skoku o
). Při použití posunutého jednotkového skoku o
![]() a s použitím věty o posunutí lze dospět k obrazu
a s použitím věty o posunutí lze dospět k obrazu
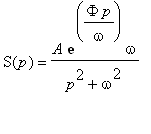 . Na následujících obrázcích jsou uvedeny oba typy signálů. Čtenář si může ověřit, že výsledek následujícího odvození nezávisí na použitém typu obrazu funkce
. Na následujících obrázcích jsou uvedeny oba typy signálů. Čtenář si může ověřit, že výsledek následujícího odvození nezávisí na použitém typu obrazu funkce
![]() .
.
| > | plot(Heaviside(t-Pi/5)*5*sin(t-Pi/5),t=-1..8,title=`sin(t-x)*1(t-x)`,thickness=3); |
| > | plot(Heaviside(t)*5*sin(t-Pi/5),t=-1..8,title=`sin(t-x)*1(t)`,thickness=3); |
![[Maple Plot]](images_odezva/odezva48.gif)
![[Maple Plot]](images_odezva/odezva49.gif)
Jestliže budeme chtít znát předmět funkce
![]() , nemůžeme to provést takto.
, nemůžeme to provést takto.
| > | invlaplace(S*F(p),p,t); |

V tomto obecném případě to samozřejmě přímo nepůjde, protože
![]() je zadaná obecně. Pro výpočet lze použít vzpomenutou větu o reziduích. Neznáme však singulární body funkce
je zadaná obecně. Pro výpočet lze použít vzpomenutou větu o reziduích. Neznáme však singulární body funkce
![]() , známe pouze póly obrazu budícího signálu. Budeme tedy moci odvodit vynucenou složku výstupního signálu pomocí reziduí právě v těchto pólech. Jak víme, vlastní složka odezvy je daná póly funkce
, známe pouze póly obrazu budícího signálu. Budeme tedy moci odvodit vynucenou složku výstupního signálu pomocí reziduí právě v těchto pólech. Jak víme, vlastní složka odezvy je daná póly funkce
![]() a pro stabilní systém postupně vymizí (přechodový děj).
a pro stabilní systém postupně vymizí (přechodový děj).
| > | readlib(residue): r1:=simplify(convert(simplify(residue(F(p)*S*exp(p*t), p=I*omega)),exp)); r2:=simplify(convert(simplify(residue(F(p)*S*exp(p*t), p=-I*omega)),exp)); |
![]()
![]()
Pro výpočet residua použijeme limitu
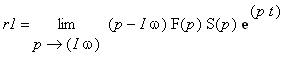 a
a
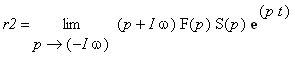 . Tuto limitu lze jednoduše vypočítat i "v ruce". V případě Maple se o to nemusíme starat.
. Tuto limitu lze jednoduše vypočítat i "v ruce". V případě Maple se o to nemusíme starat.
| > | simplify(limit((p-I*omega)*F(p)*S*exp(p*t), p=I*omega)); #simplify(convert(%,exp)); simplify(limit((p+I*omega)*F(p)*S*exp(p*t), p=-I*omega)); |
![]()
![]()
Připomeňme pouze, že vztah pro výpočet rezidua ve vícenásobném pólu je poněkud složitější (viz. např. [LA]). Tento případ však již přasahuje rámec tohoto textu, navíc díky Maple není důležitý.
Jak bylo žečeno, stejně by se počítala i rezidua pro výpočet přirozené složky odezvy
![]() , ale rezidua by se počítala v pólech přenosové fynkce
, ale rezidua by se počítala v pólech přenosové fynkce
![]() . Pokud by však některý z pólů měl reálnou část větší než nula, evidentně by limita pro výpočet příslušného rezidua rostla, díky členu
. Pokud by však některý z pólů měl reálnou část větší než nula, evidentně by limita pro výpočet příslušného rezidua rostla, díky členu
![]() (
(
![]() ), nadevšechny meze a obvod by byl tudíž nestabilní, jak bylo dříve poznamenáno.
), nadevšechny meze a obvod by byl tudíž nestabilní, jak bylo dříve poznamenáno.
H
ledanou funkci dostaneme součtem jednotlivých reziduí
![]() . Jelikož ve většině případů bude přenosová funkce obvodu F(p) racionální funkcí, můžeme ještě uplatnit její vlastnosti (
. Jelikož ve většině případů bude přenosová funkce obvodu F(p) racionální funkcí, můžeme ještě uplatnit její vlastnosti (
![]() ):
):
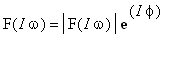 a platí:
a platí:
![]() ;
;
![]() , tj.
, tj.
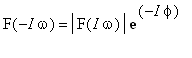
Jestliže do úpravy výsledné funkce vememe v potaz i tyto vlastnosti dostaneme následující výraz.
| > | o[v](t):=simplify(subs(F(I*omega)=abs(F(I*omega))*exp(I*phi),r1)+subs(F(-I*omega)=abs(F(I*omega))*exp(-I*phi),r2)); |
![]()
Je patrné, že vynucená (ustálená) složka odezvy obvodu na sinusový signál je rovněž sinusová (vynucená složka, která je periodickou funkcí se nazývá
ustálenou složkou
odezvy). Poměr amplitud vstupního a výstupního signálu je dán absolutní hodnotou
![]() , zatímco rozdíl jejich fázových posuvů je dán vztahem
, zatímco rozdíl jejich fázových posuvů je dán vztahem
![]() . Funkce
. Funkce
![]() se pak nazývá
kmitočtová charakteristika
obvodové funkce
se pak nazývá
kmitočtová charakteristika
obvodové funkce
![]() . Složky kmitočtové charakteristiky
. Složky kmitočtové charakteristiky
![]() a
a
![]() jsou pak
amplitudovou
a
fázovou charakteristikou
obvodové funkce
jsou pak
amplitudovou
a
fázovou charakteristikou
obvodové funkce
![]() . Podobně lze odvodit, že pro obecný periodický budící signál s periodou
. Podobně lze odvodit, že pro obecný periodický budící signál s periodou
![]() , je vynucená složka odezvy také periodickou funkcí se shodnou periodou.
, je vynucená složka odezvy také periodickou funkcí se shodnou periodou.
V posledním vztahu jsme přešli (v případě ustálené složky) od Laplaceovy transformace k transformaci Fourierově -- náhradou
![]() za
za
![]() ve vztahu pro přenos obvodu
ve vztahu pro přenos obvodu
![]() . Mezi definičními vztahy těchto transformací a rovměž jejichž vlastnostmi a obrazy stejných funkcí platí velmi úzký vztah (viz definiční vztahy obou transformací). Dále je zřejmé, že vztah pro přenos obvodu
. Mezi definičními vztahy těchto transformací a rovměž jejichž vlastnostmi a obrazy stejných funkcí platí velmi úzký vztah (viz definiční vztahy obou transformací). Dále je zřejmé, že vztah pro přenos obvodu
![]() dostaneme i pomocí symbolicko-komplexního vyjádření, což je velmi důležitá souvislost s FT.
Rovnice obvodu v harmonickém ustáleném stavu, formulované pomocí symbolicko-komplexní metody, jsou totiž zároveň rovnicemi Fourierových obrazů napěťových a proudových odezev při přechodových jevech.
FT napětí a proudů vyjadřuje vztah mezi odezvami v časové oblasti (souvislost FT s LT) a kmitočtovými odezvami -- charakteristikmi.
Lze totiž ukázat, že pro Fourierovy obrazy napětí a proudů platí Kirchhoffovy zákony a že při nulových počátečních podmínkách platí pro Fourierův obraz napětí a proudu dvojpólu Ohmův zákon:
dostaneme i pomocí symbolicko-komplexního vyjádření, což je velmi důležitá souvislost s FT.
Rovnice obvodu v harmonickém ustáleném stavu, formulované pomocí symbolicko-komplexní metody, jsou totiž zároveň rovnicemi Fourierových obrazů napěťových a proudových odezev při přechodových jevech.
FT napětí a proudů vyjadřuje vztah mezi odezvami v časové oblasti (souvislost FT s LT) a kmitočtovými odezvami -- charakteristikmi.
Lze totiž ukázat, že pro Fourierovy obrazy napětí a proudů platí Kirchhoffovy zákony a že při nulových počátečních podmínkách platí pro Fourierův obraz napětí a proudu dvojpólu Ohmův zákon:
U(I
![]() ) =
Z
I(I
) =
Z
I(I
![]() ),
atd.
),
atd.
Této významné fyzikální interpretace FT se plně využívá v teorii obvodů (např. vztah mezi kmitočtovou charakteristikou a časovou odezvou -- znám-li póly přenosové funkce lineárního stabilního systému, zanám jak jeho kmitočtové charakteristiky, tak časové odezvy). Naproti tomu řešení diferenciálních rovnic obvodu pomocí FT je v porovnání s LT náročnšjší a navíc lze LT řešit větší obor i poměrně složitých případů.
V závěru je nutné upozornit na některé "matematické souvislosti" předchozích úvah a závěrů. Mezi matematickým charakterem Laplaceova a Fourierova je totiž značný rozdíl. Laplaceův obraz
![]() je holomorfní funkcí\footnote{co to je} komplexní proměnné, jež nemá fyzikální význam. Naproti tomu Fourierův obraz
je holomorfní funkcí\footnote{co to je} komplexní proměnné, jež nemá fyzikální význam. Naproti tomu Fourierův obraz
![]() je spojitou funkcí pouze pro reálné hodnoty proměnné
je spojitou funkcí pouze pro reálné hodnoty proměnné
![]() , jež mají fyzikální význam jako úhlový kmitočet a pro imaginární hodnoty
, jež mají fyzikální význam jako úhlový kmitočet a pro imaginární hodnoty
![]() nemusí obraz
nemusí obraz
![]() existovat.
existovat.
Nahradit
![]() za
za
![]() tudíž nelze ve všech případech. Je třeba, aby póly funkce
tudíž nelze ve všech případech. Je třeba, aby póly funkce
![]() (v našem případě
(v našem případě
![]() ) byly v levé polorovině a to pro takové funkce, jejichž předmět -- funkce
) byly v levé polorovině a to pro takové funkce, jejichž předmět -- funkce
![]() bude rovna nule pro
bude rovna nule pro
![]() .
.
Druhá podmínka (
![]() pro
pro
![]() ) vyplývá z definice LT, resp. z nutných podmínek pro předmět (funkci
) vyplývá z definice LT, resp. z nutných podmínek pro předmět (funkci
![]() ), na kterou má být transformace uplatněna, tj. funkce
), na kterou má být transformace uplatněna, tj. funkce
![]() musí být standardního typu.
musí být standardního typu.
Pozn:
P
ředmět standardního typu je každá komplexní funkce reálné proměnné má-li tyto tři vlastnosti: (1) je po částech spojitá na intervalu <0,
![]() ), (2) je exponenciálního řádu a (3) rovná se nule pro všechna
), (2) je exponenciálního řádu a (3) rovná se nule pro všechna
![]() . (Zkráceně: funkce
. (Zkráceně: funkce
![]() se nazývá exponenciálního řádu s indexem růstu
se nazývá exponenciálního řádu s indexem růstu
![]() , existuje-li takové
, existuje-li takové
![]() a číslo
a číslo
![]() , že nerovnost
, že nerovnost
![abs(f(t)) < M*exp(xi[1]*t)](images_odezva/odezva107.gif) , (nebo se rovná) platí pro všechna
, (nebo se rovná) platí pro všechna
![]() , pro která je funkce definována).
, pro která je funkce definována).
Uvědomme si, že exponenciála
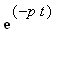 definičního integrálu LT by pro nekonečné záporné hohnoty
definičního integrálu LT by pro nekonečné záporné hohnoty
![]() rostla nadevšechny meze, tudíž je dolní mez integrálu rovna nule a tudíž i předmět musí být v tomto oboru (
rostla nadevšechny meze, tudíž je dolní mez integrálu rovna nule a tudíž i předmět musí být v tomto oboru (
![]() ) roven nule, abychom vyločili stejný obraz pro různé předměty.
) roven nule, abychom vyločili stejný obraz pro různé předměty.
To, že póly obrazu
![]() musí pro přechod k Fourierově transformaci (
musí pro přechod k Fourierově transformaci (
![]() ) ležet v levé polorovině koplexní roviny lze odvodit čistě matematicky nebo to lze jednoduše zjistit z teorie obvodů. Symbolicko-komplexní metody lze použít jen pro řešení asymptoticky stabilních obvodů -- v ustáleném stavu existuje při harmonickém buzení jen jediný harmonický ustálený stav nezávislý na počátečních podmínkách. Přenosové funkce takových obvodů však mají póly v levé polorovině.
) ležet v levé polorovině koplexní roviny lze odvodit čistě matematicky nebo to lze jednoduše zjistit z teorie obvodů. Symbolicko-komplexní metody lze použít jen pro řešení asymptoticky stabilních obvodů -- v ustáleném stavu existuje při harmonickém buzení jen jediný harmonický ustálený stav nezávislý na počátečních podmínkách. Přenosové funkce takových obvodů však mají póly v levé polorovině.
Skutečnost, že u nestabilních obvodů nelze pro řešení použít symbolicko-komplexní metody se můžeme přesvědčit na velmi jednoduchém obvodu, např. netlumeného sériového rezonančního LC obvodu napájeného harmonickým signálem (póly charakteristické funkce leží na imaginární ose). Je zřejmé, že v tomto případě obvod nedosáhne ustáleného stavu, který jako jediný by bylo možno řešit symbolicko-komplexní metodou. Je nutné rozlišit dva případy: (1) budicí kmitočet se nerovná kmitočtu rezonančnímu, pak je proud
![]() vyjádřen součtem dvou harmonických funkcí, z nichž jedna má kmitočet
vyjádřen součtem dvou harmonických funkcí, z nichž jedna má kmitočet
![]() a druhá kmitočet buzení
a druhá kmitočet buzení
![]() . Je tedy omezenou funkcí, narozdíl od případu (2), kdy
. Je tedy omezenou funkcí, narozdíl od případu (2), kdy
![]() . Obvod není regulární a jeho řešení není zdaleka jednoduché. Tyto skutečnosti samozřejmě není možné zjistit pomocí symbolicko-komplexní metody, jak bylo řečeno, ale je nutné použít LT nebo řešit přímo příslušnou diferenciální rovnici.
. Obvod není regulární a jeho řešení není zdaleka jednoduché. Tyto skutečnosti samozřejmě není možné zjistit pomocí symbolicko-komplexní metody, jak bylo řečeno, ale je nutné použít LT nebo řešit přímo příslušnou diferenciální rovnici.
Toto je důvod, proč např. střídavá analýza v programu SPICE dává pro nestabilní obvody naprosto zavádějící výsledky! Jestli získané kmitočtové charakteristiky jsou opravdu skutečnými charakteristikami analyzovaného obvodu nebo jen vykreslením matematické funkce bez vatahu na reálný systém se musíme ujistit z polohy pólů přenosové funkce.
Na závěr uvedeme ještě matematický příklad nesprávného použití FT na funkci jednotkového skoku (
![]() ). Lapaceův obraz této funkce je
). Lapaceův obraz této funkce je
![]() =
=
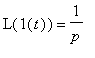 a bylo by chybou domnívat se, že Fourierův obraz dostaneme prostým dosazením dosazením
a bylo by chybou domnívat se, že Fourierův obraz dostaneme prostým dosazením dosazením
![]() za
za
![]() v Laplaceově obrazu. Neplatí totiž výše uvedené podmínky -- pól funkce
v Laplaceově obrazu. Neplatí totiž výše uvedené podmínky -- pól funkce
![]() leží na imaginární ose. O neexistenci Fourierova obrazu se přesto můžeme ještě přesvědčit výpočtem definičního integrálu FT
leží na imaginární ose. O neexistenci Fourierova obrazu se přesto můžeme ještě přesvědčit výpočtem definičního integrálu FT
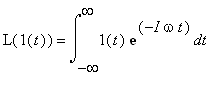 =
=
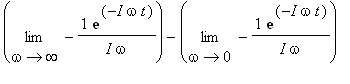 . Jelikož limita pro
. Jelikož limita pro
![]() neexistuje, nemůže existovat ani Fourierův obraz jednotkového skoku a tudíž ani funkce
neexistuje, nemůže existovat ani Fourierův obraz jednotkového skoku a tudíž ani funkce
![]() nemůže být fourierovským předmětem standardního typu -- integrál
nemůže být fourierovským předmětem standardního typu -- integrál
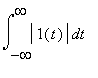 nemá konečnou hodnotu.
nemá konečnou hodnotu.
Zde je potvrzení výše uvedených skutečností.
| > | Int(Heaviside(t)*exp(-I*omega*t),t = -infinity .. infinity):%=value(%); |
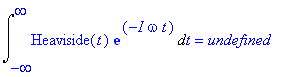
| > | Int(abs(Heaviside(t)),t = -infinity .. infinity):%=value(%); |

Podobně není definován ani fourierův obraz pro signál
![]() -- (
-- (
 ), což lze rozšířit na všechny periodické funkce. Fourierův obraz lze hledat jen u takových funkcí (analogových signálů), které mají konečnou energii, tj.
), což lze rozšířit na všechny periodické funkce. Fourierův obraz lze hledat jen u takových funkcí (analogových signálů), které mají konečnou energii, tj.
 musí být konečné čislo.
musí být konečné čislo.
| > | Int(sin(w*t)*exp(-I*omega*t),t = -infinity .. infinity):%=value(%); |
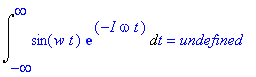
Uvědomme si jaké jsou definiční vztahy Fourierovy transformace (vztahem
![]() míníme komplexní funkci reálné proměnné
míníme komplexní funkci reálné proměnné
![]() , kterou většinou zapisujeme následujícím způsobem
, kterou většinou zapisujeme následujícím způsobem
![]() .
.
| > | G(omega)=convert(fourier(g(t),t,omega),int); g(t)=convert(invfourier(G(omega),omega,t),int); |

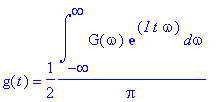
Pro účely teorie obvodů by však bylo velmi výhodné, kdyby obrazy výše uvedených funkcí existovaly. Proč? ..... Jak se to zařídí? .....
| > | fourier(A*exp(I*omega0*t),t,omega) assuming omega0>0; |
| > | fourier(A*cos(omega0*t),t,omega) assuming omega0>0; |
| > | fourier(A*sin(omega0*t),t,omega) assuming omega0>0; |
![]()
![]()
![]()
Tyto vztahy lze poměrně snadno odvodit při znalosti spektra konstantního signálu (
![]() , což lzde dokázat zpětnou fransformací
, což lzde dokázat zpětnou fransformací
![]() ) a použitím věty o kmitočtovém posunu
) a použitím věty o kmitočtovém posunu
![]()
Lze tak získat obraz komplexní exponencialy.
![]() což lze potvrdit zpětnou transformací
což lze potvrdit zpětnou transformací
![]()
Odtud již lze napsat i ostatní vztahy (pro funkce sin a cos), pokud uvážíme, že
![]() . Podobně odvodit i vztah pro obecný periodický signál
. Podobně odvodit i vztah pro obecný periodický signál
![]() kde
kde
![]()
Jaký je tedy vztah mezi spektrem periodického signálu vypočteným pomocí Fourierovy transformace a koeficienty jeho Fourierova rozvoje. Například pro spektrum funkce
![]() platí výše uvedený vztah. Vzhledem k~tomu, že
platí výše uvedený vztah. Vzhledem k~tomu, že
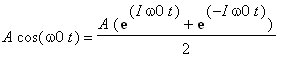 , jsou koeficienty komplexní Fourierovy řady
, jsou koeficienty komplexní Fourierovy řady
![]() =
=
![]() . Jejich grafické znázornění je uvedeno na následijícím obrázku (a). Oproti tomu spektrum stejného signálu
. Jejich grafické znázornění je uvedeno na následijícím obrázku (a). Oproti tomu spektrum stejného signálu
![]() , získané Fourierovou transformací tvoří dva Diracovy pulzy s plochou
, získané Fourierovou transformací tvoří dva Diracovy pulzy s plochou
![]() na kmitočtech
na kmitočtech
![]() a
a
![]() , jak ukazuje obrázek (b).
, jak ukazuje obrázek (b).
![[Maple Bitmap]](images_odezva/odezva159.gif)
Plocha Diracových pulzů je přitom úměrná velikosti koeficientu
![]() Fourierova rozvoje. Je-li fyzikální rozměr amplitudy
Fourierova rozvoje. Je-li fyzikální rozměr amplitudy
![]() např. [V], pak plocha tohoto pulzu má fyzikální rozměr [V * s * rad / s]=[V * rad]. Pokud tedy chceme znát velikost příslušného koeficientu
např. [V], pak plocha tohoto pulzu má fyzikální rozměr [V * s * rad / s]=[V * rad]. Pokud tedy chceme znát velikost příslušného koeficientu
![]() stačí vydělit plochu odpovídajícího Diracova pulzu členem
stačí vydělit plochu odpovídajícího Diracova pulzu členem
![]() . To také evidentní ze vztahu pro zpětnou Fourierovu transformaci. Pokud ho budeme aplikovat na dané spektrum (např. kosinusového signálu), vynásobené amplitudou
. To také evidentní ze vztahu pro zpětnou Fourierovu transformaci. Pokud ho budeme aplikovat na dané spektrum (např. kosinusového signálu), vynásobené amplitudou
![]() , dostaneme člen
, dostaneme člen
![]() násobený integrálem, udávajícím plochy obou pulzů násobené komplexními exponenciálami, tj.
násobený integrálem, udávajícím plochy obou pulzů násobené komplexními exponenciálami, tj.
![]()
![]()
Po úpravě samozřejmě dostaneme původní signál se správnou velikostí amplitudy.
| > |
| > | invfourier(%,omega,t); |
![]()
Podobně lze i následující
| > | fourier(Heaviside(t),t,omega); |
![]()
| > | invfourier(%,omega,t); |
![]()
Jelikož
 musí platit následující (
musí platit následující (
 ).
).
| > | fourier(Dirac(t),t,omega); fourier(1,t,omega); fourier(t,t,omega); |
![]()
![]()
![]()
| > |