Časové odezvy systémů se dvěma póly
Pro výše popsaný přenos lze najít pomocí zpětné Laplaceovy transformace výraz pro impulzní charakteristiku,
| > | Pt:=invlaplace(P, p, t); |
což je zřejmé, uvědomíme-li si, že lze zmíněný přenos přepsat do tvaru sočtu částečných zlomků.
| > | P=convert(P,parfrac,p); |
| (3.4.1) |
Pro obecně zadané komlexně sdružené póly přenosu (![]() ,
, ![]() ), lze potom impulzní charakteristiku vyjádřit ve tvaru:
), lze potom impulzní charakteristiku vyjádřit ve tvaru:
| > | Ptk:=evalc(subs({p1=sigma[p]+I*omega[p],p2=sigma[p]-I*omega[p]},Pt)); |
![`/`(`*`(K, `*`(exp(`*`(t, `*`(sigma[p]))), `*`(sin(`*`(t, `*`(omega[p])))))), `*`(omega[p]))](images_pl/pol_nul_78.gif) |
(3.4.2) |
Úpravou tvaru ptt (vyjádřením reálné části) jsme získali předpokládaný výsledek. Je zřejmé, že imaginární část reálného signálu (odezvy) musí být nulová.
Dříve než si ukážeme konkrétní průběh impulzní charakteristiky, zastavme se u daného výsledku impuzní charakteristiky Re(ptt). Je vidět, že přítomnost komplexně sdružených pólů v přenosové funkci má za následek výskyt tlumené harmické složky ve výstupním signálu (přirozené odezvě). Kmitočet sinusové složky je roven přirozenému (vlastnímu) kmitočtu ![]() ;
; ![]() se nazývá absolutním činitelem tlumení. Jak je z vidět ze vztahu Re(ptt), musí být pro stabilní systém tento činitel záporný, resp. musí platit
se nazývá absolutním činitelem tlumení. Jak je z vidět ze vztahu Re(ptt), musí být pro stabilní systém tento činitel záporný, resp. musí platit ![]() .
.
Nyní roznásobíme výraz pro přenos a dosadíme za kořeny výrazy ![]() ,
, ![]() .
.
| > | Pk:=K/expand(subs({p1=sigma[p]+I*omega[p],p2=sigma[p]-I*omega[p]},denom(P))); |
| (3.4.3) |
Provedeme nové přiřazení, které jak dále ukážeme bude výhodné pro charakterizaci přenosů s koplexními póly .
| > | omega[0]^2=omega[p]^2+sigma[p]^2;
xi=abs(sigma[p])/omega[0]; Q=omega[0]/2/abs(sigma[p]); |
Je patrné, že ![]() vyjadřuje modul pólu (|p1| = |p2|). Tento kmitočet je vlastně zlomovým kmitočtem modulové charakteristiky stabilního systému, přičemž si musíme uvědomit, žě v případě koplexně združeného pólu zaávisí tvar kmitočtových charakteristik jak na
vyjadřuje modul pólu (|p1| = |p2|). Tento kmitočet je vlastně zlomovým kmitočtem modulové charakteristiky stabilního systému, přičemž si musíme uvědomit, žě v případě koplexně združeného pólu zaávisí tvar kmitočtových charakteristik jak na ![]() , tak na
, tak na ![]() nebo
nebo ![]() (při dvojnásobném reálném pólu vykazuje modul přenosu pro
(při dvojnásobném reálném pólu vykazuje modul přenosu pro ![]() pokles o 6dB). Jelikož výše zmíněný absolutní činitel tlumení
pokles o 6dB). Jelikož výše zmíněný absolutní činitel tlumení ![]() není výhodné udávat, protože bychom jej museli udávat spolu s vlastním kmitočtem
není výhodné udávat, protože bychom jej museli udávat spolu s vlastním kmitočtem ![]() , definujeme činitel
, definujeme činitel ![]() nebo častěji Q. Činitel
nebo častěji Q. Činitel ![]() se pro stabilní systém (
se pro stabilní systém (![]() < 0) nazývá relatinní činitel tlumení a činitel Q činitel jakosti příslušející dané dvojici komlexně sdružených pólů. Vztah mezi zlomovým kmitočtem
< 0) nazývá relatinní činitel tlumení a činitel Q činitel jakosti příslušející dané dvojici komlexně sdružených pólů. Vztah mezi zlomovým kmitočtem ![]() a
a ![]() je zřejný z následujících rovností, nebo názorněji z níže uvedených obrázků. Činitel jakosti Q navíc velmi názorně vystihuje průběh modulové charakteristiky, jak dále ukážeme. Při zlomovém kmitočtu může modulová charakteristika vykazovat jak překmit, tak pokles oproti "asymptotické" hodnotě, přičemž skutečná hodnota modulu přenosu při tomto kmitočtu je Q násobkem "asymptotické" hodnoty.
je zřejný z následujících rovností, nebo názorněji z níže uvedených obrázků. Činitel jakosti Q navíc velmi názorně vystihuje průběh modulové charakteristiky, jak dále ukážeme. Při zlomovém kmitočtu může modulová charakteristika vykazovat jak překmit, tak pokles oproti "asymptotické" hodnotě, přičemž skutečná hodnota modulu přenosu při tomto kmitočtu je Q násobkem "asymptotické" hodnoty.
| (3.4.4) |
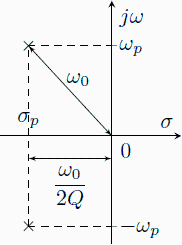
Předpokládejme kořeny v levé polorovině (![]() , tj.
, tj. ![]() ). Výraz pro přenos nyní můžeme přepsat do následujícího tvaru.
). Výraz pro přenos nyní můžeme přepsat do následujícího tvaru.
| > | Pq:=subs({omega[p]^2=omega[0]^2-(omega[0]/2/Q)^2,sigma[p]=-omega[0]/2/Q},Pk);
|
![`/`(`*`(K), `*`(`+`(`*`(`^`(p, 2)), `/`(`*`(p, `*`(omega[0])), `*`(Q)), `*`(`^`(omega[0], 2)))))](images_pl/pol_nul_103.gif) |
(3.4.5) |
Pro kořeny platí:
| > | p12:=solve(denom(Pq),p); |
| (3.4.6) |
Podle hodnoty činitele jakosti Q můžeme provést následující dělení (pro jednoduchost volíme pro všechny případy stejný kmitočet ![]() = 1000, aniž bychom se dopustili jakéhokoliv omezení obecnosti).
= 1000, aniž bychom se dopustili jakéhokoliv omezení obecnosti).
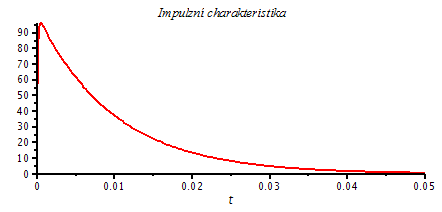
1. Pro Q < 1/2, resp. ![]() dostaneme dva různé reálné póly, pro něž má impulzní charakteristika níže uvedený tvar a průběh. Pokud bychom chtěli použít vyjádření pomocí výše uvedených parametrů
dostaneme dva různé reálné póly, pro něž má impulzní charakteristika níže uvedený tvar a průběh. Pokud bychom chtěli použít vyjádření pomocí výše uvedených parametrů ![]() a
a ![]() pro charakterizaci dvou různých pólů ležících na záporné réálné ose, lze to učinit následovně:
pro charakterizaci dvou různých pólů ležících na záporné réálné ose, lze to učinit následovně:
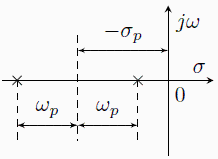
| > | Q1:=1/10;
xi=1/(2*Q1); omega[0]=1000; 'p12'=evalf(subs({Q=Q1,omega[0]=1000},[p12])); Pt1:=evalf(subs({K=1000^2,p1=subs({Q=Q1,omega[0]=1000},[p12])[1],p2=subs({Q=Q1,omega[0]=1000},[p12])[2]},Pt)); plot(Pt1,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
 |
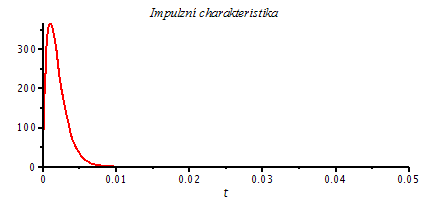
2. Pro Q = 1/2, resp. ![]() dostaneme dva stejné reálné póly (dvojnásobný pól), pro něž má impulzní charakteristika následující tvar a průběh. Pro tento případ však musíme nejprve přepočítat obecný vztah pro časovou odezvu Pt z upraveného vztahu pro přenos. Časová odezva právě ještě nevykazuje kmitavou odezvu, modulová charakteristika právě nebude vykazovat překmit a pokles chrakteristiky v bodě zlomu je 6 dB.
dostaneme dva stejné reálné póly (dvojnásobný pól), pro něž má impulzní charakteristika následující tvar a průběh. Pro tento případ však musíme nejprve přepočítat obecný vztah pro časovou odezvu Pt z upraveného vztahu pro přenos. Časová odezva právě ještě nevykazuje kmitavou odezvu, modulová charakteristika právě nebude vykazovat překmit a pokles chrakteristiky v bodě zlomu je 6 dB.
| > | P2:=subs(p2=p1,P);
Pt2:=invlaplace(P2, p, t); Q2:=1/2; xi=1/(2*Q2); omega[0]=1000; 'p12'=evalf(subs({Q=Q2,omega[0]=1000},[p12])); Pt2:=evalf(subs({K=1000^2,p1=subs({Q=Q2,omega[0]=1000},[p12])[1],p2=subs({Q=Q2,omega[0]=1000},[p12])[2]},Pt2)); plot(Pt2,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
 |
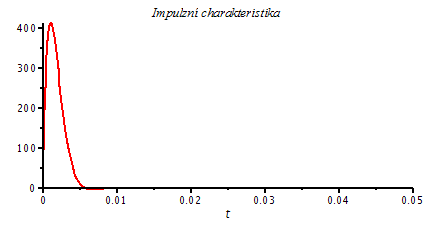
3. Pro Q > 1/2, resp. ![]() dostaneme dva komplexně sdružené póly se zápornou reálnou částí, pro něž má impulzní charakteristika kmitavý, harmonický, tlumený průběh. Jak rychle se tato kmitavá odezva utlumí, záleží na velikosti činitele tlumení, resp. na hodnotě činitele jakosti Q. Je samozřejmé, že se při měnící hodnotě
dostaneme dva komplexně sdružené póly se zápornou reálnou částí, pro něž má impulzní charakteristika kmitavý, harmonický, tlumený průběh. Jak rychle se tato kmitavá odezva utlumí, záleží na velikosti činitele tlumení, resp. na hodnotě činitele jakosti Q. Je samozřejmé, že se při měnící hodnotě ![]() , bude měnit i tvar příslušné modulové charakteristiky (při vzrůstajícím Q se bude zvětšovat i velikost "překmitu" na modulvé charakteristice). Zde je nutné ještě rozlišovat několik případů.
, bude měnit i tvar příslušné modulové charakteristiky (při vzrůstajícím Q se bude zvětšovat i velikost "překmitu" na modulvé charakteristice). Zde je nutné ještě rozlišovat několik případů.
> 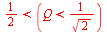 Tehdy je
Tehdy je ![sigma[n]](images_pl/pol_nul_128.gif) >
> ![omega[n]](images_pl/pol_nul_129.gif) a tlumení je ještě velké
a tlumení je ještě velké 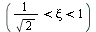 , že se signál prakticky dříve utlumí, než dojde k periodickým kmitům (vzniká jeden až dva překmity). Na tomto příkladě je velmi dobře vidět důvod a výhody definice činitele jakosti, který udává "velikost tlumení" relativně k délce periodě vlastních kmitů, oproti absolutnímu činiteli tlumení, který je vztažen pouze k času t. Modulová charakteristika nebude ještě vykazovat překmit.
, že se signál prakticky dříve utlumí, než dojde k periodickým kmitům (vzniká jeden až dva překmity). Na tomto příkladě je velmi dobře vidět důvod a výhody definice činitele jakosti, který udává "velikost tlumení" relativně k délce periodě vlastních kmitů, oproti absolutnímu činiteli tlumení, který je vztažen pouze k času t. Modulová charakteristika nebude ještě vykazovat překmit.
-
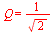 Toto je zvláštní případ, kdy
Toto je zvláštní případ, kdy ![sigma[n]](images_pl/pol_nul_132.gif) =
= ![omega[n]](images_pl/pol_nul_133.gif) , resp.
, resp. 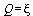 . Impulzní charakteristika je sice méně tlumena než v předchozím případě. Tlumení je však stále velké (
. Impulzní charakteristika je sice méně tlumena než v předchozím případě. Tlumení je však stále velké (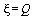 ), takže opět dojde jen k jednomu, dvěma překmitům. Modulová charakteristika ještě nebude vykazovat překmit a pokles chrakteristiky v bodě zlomu je 3dB. Jedná se o tzv. Maximálně plochou modulovou chrakteristiku.
), takže opět dojde jen k jednomu, dvěma překmitům. Modulová charakteristika ještě nebude vykazovat překmit a pokles chrakteristiky v bodě zlomu je 3dB. Jedná se o tzv. Maximálně plochou modulovou chrakteristiku.
-
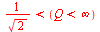 Tehdy je
Tehdy je ![`<`(sigma[n], omega[n])](images_pl/pol_nul_137.gif) a tlumení je již malé natolik
a tlumení je již malé natolik 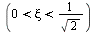 , že je na impulzní charakteristice zřetelně vidět přítomnost harmonické složky. Modulová charakteristika bude vykazovat překmit, tak jak bylo ukázáno výše.
, že je na impulzní charakteristice zřetelně vidět přítomnost harmonické složky. Modulová charakteristika bude vykazovat překmit, tak jak bylo ukázáno výše.
| (3.4.7) |
Nyní následují ukázky k jednotlivým bodům.
| > | Q3a:=0.6;
xi=1/(2*Q3a); omega[0]=1000; 'p12'=evalf(subs({Q=Q3a,omega[0]=1000},[p12])); Pt3a:=evalc(subs({K=1000^2,p1=subs({Q=Q3a,omega[0]=1000},[p12])[1],p2=subs({Q=Q3a,omega[0]=1000},[p12])[2]},Pt)); plot(Pt3a,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
 |
| > | Q3b:=1/sqrt(2);
xi=1/(2*Q3b); omega[0]=1000; 'p12'=evalf(subs({Q=Q3b,omega[0]=1000},[p12])); Pt3b:=evalf(evalc(subs({K=1000^2,p1=subs({Q=Q3b,omega[0]=1000},[p12])[1],p2=subs({Q=Q3b,omega[0]=1000},[p12])[2]},Pt))); plot(Pt3b,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
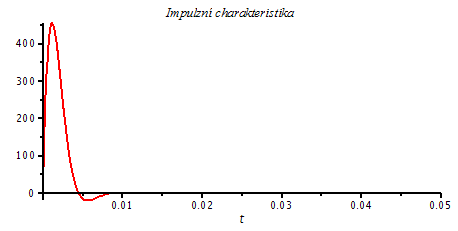 |
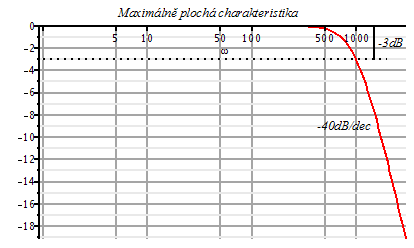
Pro tento případ ukážeme navíc odpovídající průběh modulové chrakteristiky přenosu - maximálně ploché.
| > | Pf:=evalc(abs(subs({Q=Q3b,omega[0]=1000,K=1000^2,p=I*omega},Pq)));
pl:=semilogplot(20*log10(Pf),omega=1..3000,thickness=3,title=`Maximálně plochá charakteristika`,labelfont=[HELVETICA,8],axesfont=[HELVETICA,8],thickness=2,gridlines=true): t1 := textplot([1500,-1.5,`-3dB`],align=RIGHT): t2 := textplot([1500,-9,`-40dB/dec`],align=LEFT): l:=line([1,-3],[2000,-3],color=black,linestyle=2): v1:=arrow([1500,0], [1500,-3], 2, 2, .2, color=black): v2:=arrow([1500,-3], [1500,0], 2, 1, .3, color=black): display(pl,l,t1,v1,v2,t2); |
 |
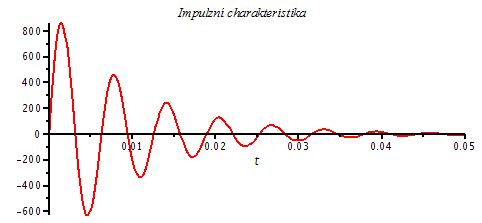
| > | Q3c:=5;
xi=1/(2*Q3b); omega[0]=1000; 'p12'=evalf(subs({Q=Q3c,omega[0]=1000},[p12])); Pt3c:=evalf(evalc(subs({K=1000^2,p1=subs({Q=Q3c,omega[0]=1000},[p12])[1],p2=subs({Q=Q3c,omega[0]=1000},[p12])[2]},Pt))); plot(Pt3c,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
 |
Důkaz uvedených skutečností
Extrémním případem je případ ryze imaginárních kořenů, jak bylo ukázáno výše a v tomto dělení je to následující případ -- čtvrtý.
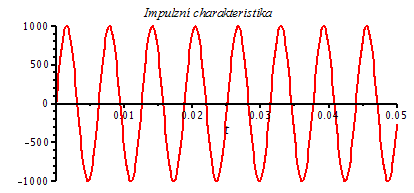
4. Pro Q = ∞ dostaneme dva komplexně sdružené, ryze imaginární póly (s nuvou reálnou částí), pro něž má impulzní charakteristika následující tvar a průběh.
| > | Q4:=infinity;
xi=0; omega[0]=1000; 'p12'=[limit(subs(omega[0]=1000,p12[1]),Q=Q4),limit(subs(omega[0]=1000,p12[2]),Q=Q4)]; Pt4:=evalf(evalc(subs({K=1000^2,p1=rhs(%)[1],p2=rhs(%)[2]},Pt))); plot(Pt4,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
 |
Námět ke zpracování: Realizujte jednotlivé případy realizovat (početně) sériovým rezonančním obvodem RLC podle výše uvedeného obrázku.
5. Posledním, i když teoretickým případem je případ komplexně sdružených kořenů s kladnou reálnou částí. V tomto případě nejde o stabilní systém, tudíž už nehovoříme o činiteli jakosti (ten by byl stejně jako činitel tlumení záporný). Pro námi zvolené hodnoty kořenů dostaneme:
| > | 'p12'=100+I*980,100-I*980;
Pt5:=evalf(evalc(subs({K=1000^2,p1=100+I*980,p2=100-I*980},Pt))); plot(Pt5,t=0..0.05,title=`Impulzní charakteristika`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
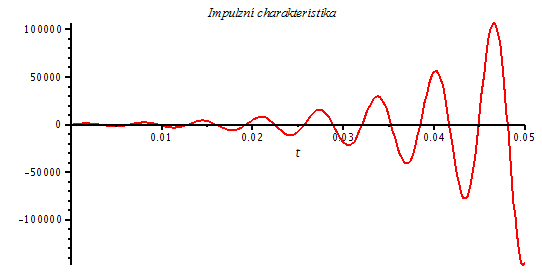 |
Systém s takovouto odezvou (jdoucí nade všechny meze) nelze, jak již bylo řečeno, v praxi realizovat. Je nutné poznamenat, že nelze realizovat ani "čistý" systém s ryze imaginárními kořeny, protože nelze v praxi tuto podmínku u "lineárních" systémů udržet vlivem fluktuace parametrů součástek. Proto je nutné tuto podmínku pro oscilující systémy zajistit, nejčastěji pomocí nelineární zpětné vazby (stabilizace amlitudy). Výstupní signál je potom "téměř" harmonický (s malým zkreslením). Bez této zpětné vazby by se systém ustálil vlivem vlastní nelilearity, např. vlivem konečného napájecího napětí, a tvar kmitů by byl silně neharmonický (relaxační kmity).