Důkaz uvedených skutečností 

Nejdříve nahradíme do vztahu pro přenos výraz za - pro výpočty je nutné rozlišit a ( je jen p-tá položka proměnné ). 

>	Pk1:=K/expand(subs({p1=sigma[p]+I*omega1[p],p2=sigma[p]-I*omega1[p]},denom(P)));

 

(3.4.1.1)

 

dosadíme za a vypočteme absolutni hodnotu prenosu (zde a v následujících výpočtech je problém v tom, že při dosazení za p se dosadí i ve výrazech a - řešení je přejít od komplexního kmitočtu v proměnné p k proměnné s)  

>	abs_Pk:=evalc(abs(K/expand(subs({p=I*omega,p1=sigma[p]+I*omega1[p],p2=sigma[p]-I*omega1[p]},denom(P)))));

 

(3.4.1.2)

 

a hledáme maximum funkce abs_Pks -- řešíme následující rovnici   

>	Diff('abs_Pk',omega)=0; reseni:=solve(diff(abs_Pk,omega),omega);

 

 

	(3.4.1.3)

 

Derivace je nulová samozřejmě v bodě , a dále pro kmitočet , pro který nastává maximum na modulové charakteristice (záporné a komplexní kmitočty samozřejmě nelze uvažovat). Tento kmitočet nazvěme . Z jeho vyjádření lze vyčíst, že "překmit" na modulové chrakteristice nastává pouze pro , . Jeli , jedná se o případ čistě imaginárních kořenů a kmitočet vlastních kmitů , se rovná zlomovému kmitočtu . O zlomovém kmitočtu však v tomto případě nelze hovořit - jde o systém na mezi stability, jak je ukázáno dále (čtvrtý případ). Čím více se hodnota blíží hodnotě vzdaluje se od zlomového kmitočtu směrem k bodu "a překmit se zmenšuje". Je-li , překmit zaniká () a to je právě případ maximálně ploché charakteristiky. Jestliže je , nelze o extrému hovořit, jelokož nastává na komplexním (nereálném) kmitočtu. To si může zvídavý čtenář ověřit na pomocí 3D grafu. To je také případ dvojice reálných kořenů, kdy platí vždy (viz pravou část náčrtu).    

>

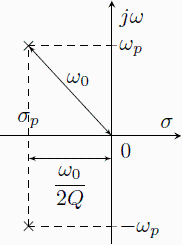
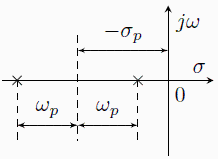
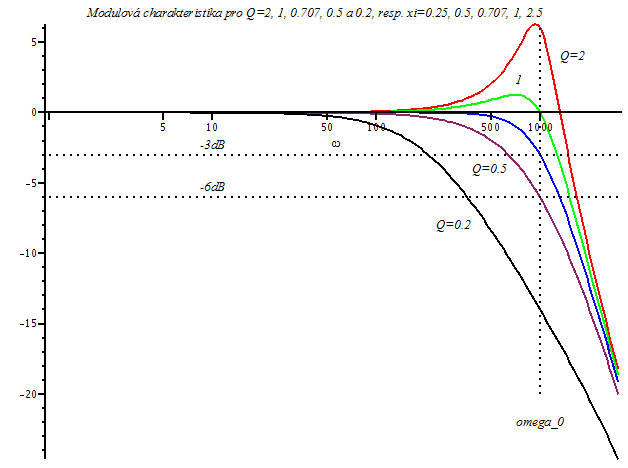
modul1:=evalc(abs(subs({Q=2,omega[0]=1000,K=1000000,p=I*omega},Pq))): modul2:=evalc(abs(subs({Q=1,omega[0]=1000,K=1000000,p=I*omega},Pq))): modul3:=evalc(abs(subs({Q=1/sqrt(2),omega[0]=1000,K=1000000,p=I*omega},Pq))): modul4:=evalc(abs(subs({Q=0.5,omega[0]=1000,K=1000000,p=I*omega},Pq))): modul5:=evalc(abs(subs({Q=0.2,omega[0]=1000,K=1000000,p=I*omega},Pq))): pl1:=semilogplot(20*log10(modul1),omega=1..3000,thickness=2,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=red): pl2:=semilogplot(20*log10(modul2),omega=1..3000,thickness=2,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=green): pl3:=semilogplot(20*log10(modul3),omega=1..3000,thickness=2,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=blue): pl4:=semilogplot(20*log10(modul4),omega=1..3000,thickness=2,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=maroon): pl5:=semilogplot(20*log10(modul5),omega=1..3000,thickness=2,title=`Modulová charakteristika pro Q=2, 1, 0.707, 0.5 a 0.2, resp. xi=0.25, 0.5, 0.707, 1, 2.5`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=black): t1 := textplot([10^3,-22,`omega_0`]): t2 := textplot([10^2.6,-8,`Q=0.2`],align=LEFT): t3 := textplot([10^2.82,-4,`Q=0.5`],align=LEFT): t4 := textplot([10^2.87,2.3,`1`]): t5 := textplot([10^3.1,4,`Q=2`],align=RIGHT): t6 := textplot([10^1,-2.8,`-3dB`],align=ABOVE): t7 := textplot([10^1,-5.8,`-6dB`],align=ABOVE): l1:=line([10^3,6],[10^3,-20],color=black,linestyle=2): l2:=line([10^0,-3],[10^3.5,-3],color=black,linestyle=2): l3:=line([10^0,-6],[10^3.5,-6],color=black,linestyle=2): display(pl1,pl2,pl3,pl4,pl5,l1,l2,l3,t1,t2,t3,t4,t5,t6,t7);

 

>

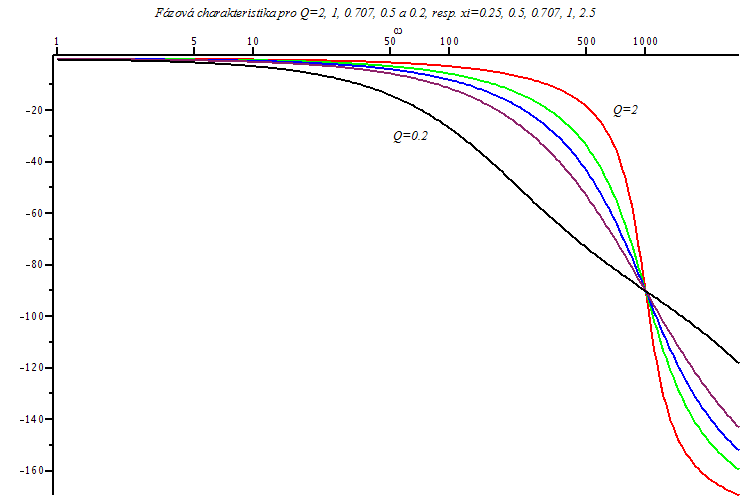
faze1:=evalc(argument(subs({Q=2,omega[0]=1000,K=1000000,p=I*omega},Pq))): faze2:=evalc(argument(subs({Q=1,omega[0]=1000,K=1000000,p=I*omega},Pq))): faze3:=evalc(argument(subs({Q=1/sqrt(2),omega[0]=1000,K=1000000,p=I*omega},Pq))): faze4:=evalc(argument(subs({Q=0.5,omega[0]=1000,K=1000000,p=I*omega},Pq))): faze5:=evalc(argument(subs({Q=0.2,omega[0]=1000,K=1000000,p=I*omega},Pq))): ph1:=semilogplot(180/Pi*faze1,omega=1..3000,thickness=2,numpoints=300,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=red): ph2:=semilogplot(180/Pi*faze2,omega=1..3000,thickness=2,numpoints=300,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=green): ph3:=semilogplot(180/Pi*faze3,omega=1..3000,thickness=2,numpoints=300,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=blue): ph4:=semilogplot(180/Pi*faze4,omega=1..3000,thickness=2,numpoints=300,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=maroon): ph5:=semilogplot(180/Pi*faze5,omega=1..3000,thickness=2,numpoints=300,title=`Fázová charakteristika pro Q=2, 1, 0.707, 0.5 a 0.2, resp. xi=0.25, 0.5, 0.707, 1, 2.5`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=black): t1 := textplot([10^2.9,-20,`Q=2`]): t2 := textplot([10^1.8,-30,`Q=0.2`]): display(ph1,ph2,ph3,ph4,ph5,t1,t2);

 

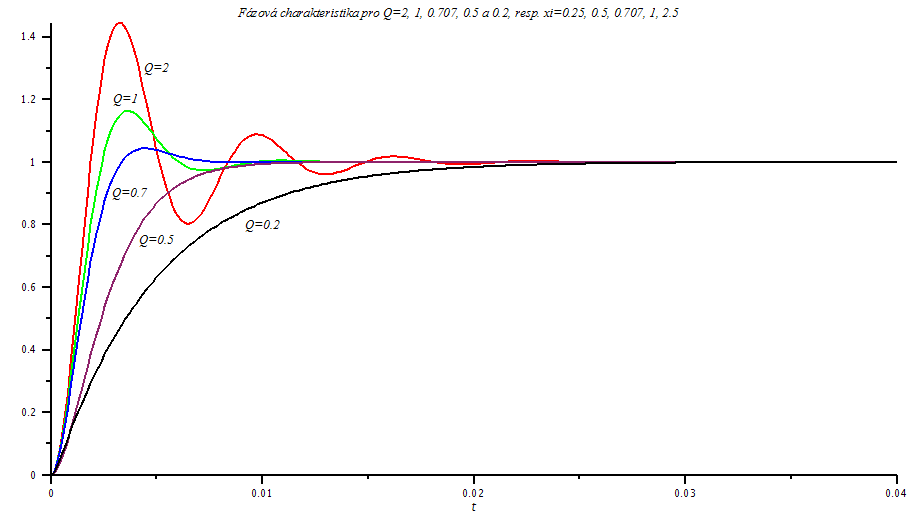
Pro úplnost ukážeme odpovídající přechodové charakteristiky (odezvu na jednotkový skok). 

>	Ptp:=invlaplace(Pq/p,p,t):

 

>	Ptp1:=subs({Q=2,omega[0]=1000,K=1000000},Ptp): Ptp2:=subs({Q=1,omega[0]=1000,K=1000000},Ptp): Ptp3:=subs({Q=1/sqrt(2),omega[0]=1000,K=1000000},Ptp): Ptp4:=subs({Q=0.5,omega[0]=1000,K=1000000},Ptp): Ptp5:=subs({Q=0.2,omega[0]=1000,K=1000000},Ptp):

 

>	Ptpi:=eval([seq(parse(cat("Ptp",i)),i=1..5)]);

 

(3.4.1.4)

 

Pozor, pro (dvojnásobný pól) je nutné vypočítat odezvu korektně (znova, tak, jako bylo uvedeno i výše).   

>	Ptp4; Ptpi[4]:=subs({p1=-1000/sqrt(2),K=1000000/2},invlaplace(P2/p, p, t));

 

 

	(3.4.1.5)

 

>

plt:=plot(Ptpi,t=0..0.04,thickness=2,numpoints=300,title=`Fázová charakteristika pro Q=2, 1, 0.707, 0.5 a 0.2, resp. xi=0.25, 0.5, 0.707, 1, 2.5`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],color=[red,green,blue,maroon,black]): t1 := textplot([0.005,1.3,`Q=2`]):t2 := textplot([0.0035,1.2,`Q=1`]):t3 := textplot([0.0037,0.9,`Q=0.7`]):t4 := textplot([0.005,0.75,`Q=0.5`]):t5 := textplot([0.01,0.8,`Q=0.2`]): display(plt,t1,t2,t3,t4,t5);

 

Pro případ si ještě ověříme polohu zlomového kmitočtu a velikost poklesu modulové charakteristiky pro tento kmitočet.  

>

Pk;

 

(3.4.1.6)

 

Dosadíme do jmenovatele přenosu a nalezneme póly přenosu. 

>	omega0:=solve(subs(sigma[p]=omega[p],denom(Pk)),p);

 

(3.4.1.7)

 

Póly musí být komplexně združené a jejich velikost musí být rovna , což pro náš případ vyjde. 

>	omega0_abs:=abs(omega0[1]);

 

(3.4.1.8)

 

Nyní vypočteme absolutní hodnotu přenosu pro a pro . Abychom dostali požadovaný výsledek, je nutno opět zavést předpoklad . 

>	Pko:=abs(K/expand(subs({p=I*omega0_abs,p1=omega[p]+I*omega[p],p2=omega[p]-I*omega[p]},denom(P)))); Pkn:=simplify(Pko) assuming omega[p]>0;

 

 

	(3.4.1.9)

 

Dále vypočteme hodnotu přenosu pro nulový kmitočet - "asyptotická" hodnota přenosu. 

>	Pk0:=abs(Limit(Pk,p=0)); Pk0:=subs({omega[0]=omega[p],sigma[0]=sigma[p]},value(Pk0));

 

 

	(3.4.1.10)

 

Nyní již lze určit pokles přenosu ve zlomovém kmitočtu a při .  

>	'Pkn/Pk0'=simplify(Pkn/subs(sigma[p]=omega[p],Pk0)) assuming omega[p]>0; 'Pkn/Pk0'=evalf(20*log10(rhs(%)));       # pokles v [dB]

 

 

	(3.4.1.11)

 

Což je výsledek který již známe z průběhu maximálně ploché modulové charakteristiky. Podíl skutečného modulu při zlomovém kmitočtu a jeho "asymptotické" hodnoty je také roven činiteli jakosti, jak bylo výše uvedeno. Tuto skutečnost lze jednoduše dokázat i pro obecný případ. 

>

Pq;

 

(3.4.1.12)

 

Dosaďme za (zlomový kmitočet) do výrazu pro modul přenosu. 

>	Pkz:=abs(subs(p=I*omega[0],Pq));

 

(3.4.1.13)

 

Tuto hodnotu vydělme "asymtotickou" hodnotou přenosu a dostaneme: 

>	'Pkz/Pk0'=simplify(subs(omega[0]=sqrt(sigma[p]^2+omega[p]^2),Pkz)/Pk0);

 

(3.4.1.14)

 

Jelikož je , je to důkaz našeho tvrzení. Nyní následuje dokončení výkladu.