Analýza rezonančního obvodu
Příklad ukázky výpočtu střídavé (ac) analýzy - určení kmitočtových charakteristik, přenosu a z něho všech přenosových charakteristik pro
![]() V,
V,
![]() k
k
![]() ,
,
![]() uF a
uF a
![]() mH.
mH.
![[Maple Bitmap]](images_maa/PraCAn_MAA121.gif)
Zadání obvodu - zdroj je opět definován jak pro střídavou, tak pro stejnosměrnou (tj. i tranzientní) analýzu.
| > | ac3:=" v1 1 0 dc 1 ac 1 R 1 2 20 L 2 3 10m C 3 0 1u .end": |
Střídavá analýza obvodu.
| > | vysl_ac3:=PraCAn(ac3, ac): |
| > | ac_char3:=simplify(subs(vysl_ac3, v("3")/v("1"))); |

Vykreslení modulové a fázové charakteristiky.
| > | plots[semilogplot](20*log10(abs(ac_char3)),f=200..1e4,labels=["f [Hz]","|P| [dB]"],thickness=3,title="Modulová charakteristika"); |
| > | plots[semilogplot](argument(ac_char3)*180/Pi,f=200..1e4,labels=["f [Hz]","phi [deg]"],thickness=3,title="Fázová charakteristika"); |
![[Maple Plot]](images_maa/PraCAn_MAA123.gif)
![[Maple Plot]](images_maa/PraCAn_MAA124.gif)
Výpočet kmitočtu maxima modulové charakteristiky (neodpovídá přesně poloze pólu - vysvětlení ve vyšším ročníku).
| > | solve(diff(evalc(abs(ac_char3)),f)); |
![]()
Výpočet vstupní impedance rezonančního obvodu jako funkce kmitočtu a určení rezonančního kmitočtu (pro
![]() ). Ten odpovídá přesně poloze pólu.
). Ten odpovídá přesně poloze pólu.
| > | Zin3:=subs(vysl_ac3, -v("1")/i("v1")); |
| > | solve(evalc(Im(Zin3))); |

![]()
Symbolický i numerický výpočet nul a pólů přenosu ze vstupu na uzel 3. Nuly přenos opět nevykazuje, nicméně póly jsou v tomto případě komplexně združené. Nakonec výpočet hodnoty pólů dělené koeficientem
![]() a jeho absolutní hodnota.
a jeho absolutní hodnota.
| > | PraCAn(ac3,PZ,symbolic,SAVE=v("3")); |
| > | zer3,pol3:=PraCAn(ac3,PZ,SAVE=v("3")); |
| > | evalf(pol3/2/Pi);abs(%[1]); |



![]()
Určení přenosu obvodu pomocí tf analýzy a z něho dále výpočet frekvenční charakteristiky (dosazením
![]() , kde
, kde
![]() ), přechodové a impulzní charakteristiky pomocí zpětné Laplaceovy transformace.
), přechodové a impulzní charakteristiky pomocí zpětné Laplaceovy transformace.
| > | vysl_tf3:=PraCAn(ac3, tf, SAVE=nodes): |
| > | P3:=subs(vysl_tf3,v("3")); |

| > | simplify(subs(s=I*2*Pi*f,P3)); |
| > | pr_char3:=inttrans[invlaplace](P3/s,s,t); |
| > | im_char3:=inttrans[invlaplace](P3,s,t); |
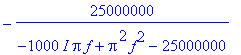
![]()
![]()
Vykreslení přechodové a impulzní charakteristiky.
| > | plot(pr_char3,t=0..5e-3,labels=["t [s]","p [V]"],thickness=3,title="Přechodová charakteristika"); |
| > | plot(im_char3,t=0..5e-3,labels=["t [s]","i [V]"],thickness=3,title="Impulzní charakteristika"); |
![[Maple Plot]](images_maa/PraCAn_MAA140.gif)
![[Maple Plot]](images_maa/PraCAn_MAA141.gif)
| > | vysl_tran3:=PraCAn(ac3, tran, SAVE=v("3")); |
![]()
| > |