Aplikace zobecněné metody uzlových napětí na obvod s OZ

Je použito schema z obr. 5.3 v lit. [1], uzly jsou očíslovány zleva doprava, vstupní má číslo 1, výstupní číslo 2.

Nejprve obnovíme základní nastavení programu a přiřadíme knihovnu pro maticové výpočty:

> restart;

> with(linalg):

Warning, the protected names norm 
and trace have been redefined and unprotected

Nadefinujeme zkrácenou admitanční matici obvodu (rozměr 5*5). K tomu použijeme buď uvedeného příkazu pro vložení celé matice po řádcích, nebo můžeme použít postup uvedený v závěru:

> Ym:=matrix([[G1,0,-G1,0,0],[0,p*C2,0,-p*C2,0],

> [-G1,0,G1+G2+p*C1,-G2,0],[0,-p*C2,-G2,G2+G3+p*C2,-G3],

> [0,0,0,-G3,G3+p*C3]]);

" Ošetříme" vstup operačního zesilovače - t.j. sečteme sloupce odpovídající uzlům vstupu (součet realizujeme odzadu):

> Ym1:=addcol(Ym,5,2);

Sloupec 5, který jsme přičetli ke sloupci 2, vypustíme:

> Ym2:=delcols(Ym1,5..5);

Nyní "ošetříme" výstup OZ - vypustíme řádek 2, odpovídající výstupnímu uzlu OZ:

> Ym3:=delrows(Ym2,2..2);

Pro výpočet přenosu potřebujeme algebraické doplňky vzniklé vypuštěním sloupce 1 a řádku 1 pro jmenovatel (odvozeno z označení uzlu na vstupu) a doplněk vzniklý vypuštěním sloupce 2 (výstupní uzel) a řádku 1 (vstupní uzel):

> d11:=minor(Ym3,1,1);

> d12:=minor(Ym3,1,2);

Pro výpočet přenosudáme oba doplňky do poměru a doplníme příslušnou mocninu (-1) v čitateli, ve jmenovateli jde o sudou, proto není uvedena. Funkce collect pouze zajišťuje "srovnání jmenovatele podle mocnin p":

> P:=(-1)^(1+2)*det(d12)/collect(det(d11),p);

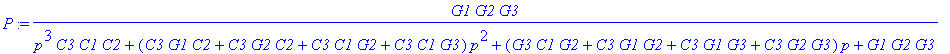
Na závěr můžeme ve výrazu nahradit hodnoty vodivostí hodnotami odporů = k tomu nám poslouží funkce subs, funkce simplify zajistí "zjednodušení" výrazu a funkce collect opět jeho srovnání podle mocnin p:

> collect(simplify(subs(G1=1/R1,G2=1/R2,G3=1/R3,P)),p);

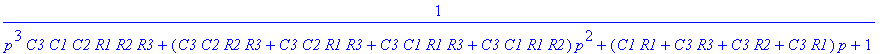
Výsledný výraz je shodný s výrazem 5.3 v [1].

Následující část naznačuje, jak lze sestavit admitanční matici postupně, pomocí dílčích kroků pro výpočet jednotlivých prvků matice.

Nejprve definujeme rozměr matice:

> mat:=matrix(5,5);

Dále definujeme jednotlivé prvky matice - např. prvek 1,1 (vstup) je součtem všech admitancí připojených na uzel 1, v našem případě pouze vodivosti G1. Prvek 2,2 (výstup) je tvořen pouze admitancí kapacitoru C2 (OZ "zařazujeme" až v dalším kroku). Pokud bychom hodnotu prvku tvořili ve více krocích, použijeme přiřazení mat[i,j:=mat[i,j]+x.

> mat[1,1]:=G1;mat[2,2]:=p*C2;

Pro kontrolu si můžeme matici v libovolném kroku vypsat následujícím příkazem. Dosud nezadané prvky jsou označeny ?.

> eval(mat);

Literatura:

[1] Davídek,V.,Laipert,M.,Vlček,M.:Analogové a číslicové filtry.Vydavatelství ČVUT, Praha 2000.