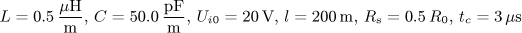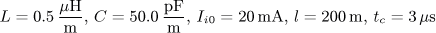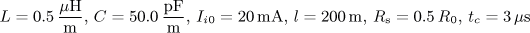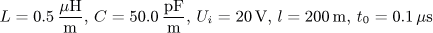Periodický neharmonický ustálený stav
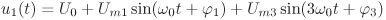
jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního napětí u2(t) a jeho efektivní hodnotu U2.
Návrat na přehled příkladů úloha 1
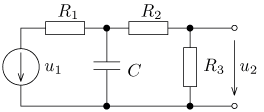
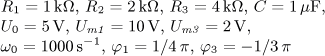
výsledek
úloha 2 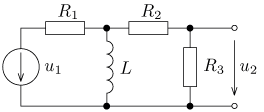
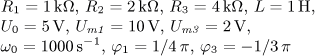
výsledek úloha 3
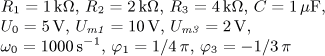
výsledek
úloha 4 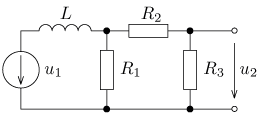
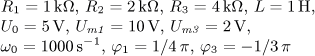
výsledek úloha 5
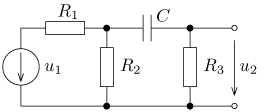
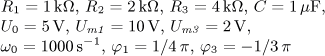
výsledek
úloha 6 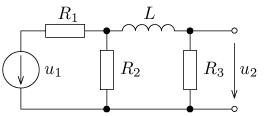
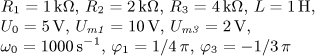
výsledek úloha 7
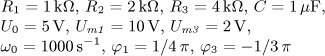
výsledek
úloha 8 
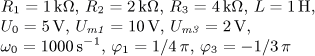
výsledek
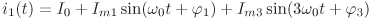
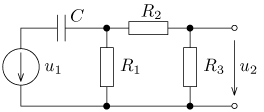
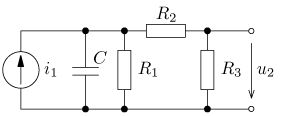
jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního napětí u2(t) a jeho efektivní hodnotu U2.
Návrat na přehled příkladů úloha 1
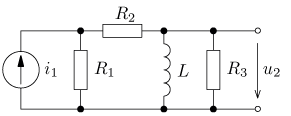
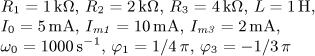
výsledek
úloha 2 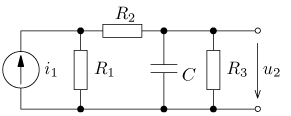
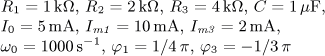
výsledek úloha 3
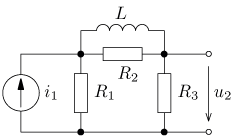
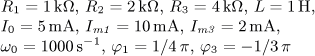
výsledek
úloha 4 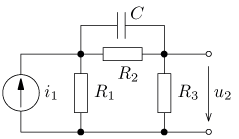
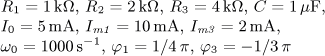
výsledek úloha 5
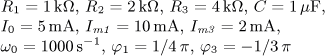
výsledek
úloha 6 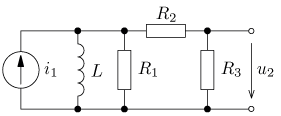
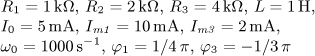
výsledek
Uvažujte první tři nenulové členy Fourierova rozvoje (včetně stejnosměrné složky,
pokud je nenulová).
obrázek a) obrázek b)
Pomůcka:
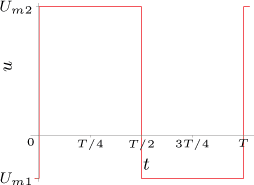
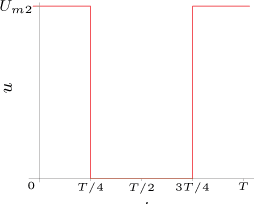
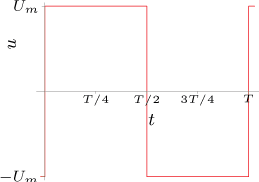
(Standardní obdélníkový průběh posunutý v amplitudě)
(Standardní obdélníkový průběh posunutý v amplitudě a umístěný souměrně k ose napětí")
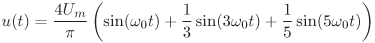
Návrat na přehled příkladů úloha 1

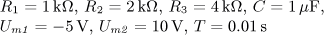
výsledek
úloha 2 
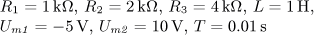
výsledek úloha 3

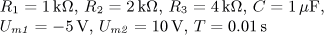
výsledek
úloha 4 
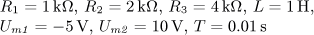
výsledek úloha 5

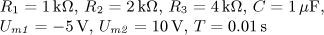
výsledek
úloha 6 
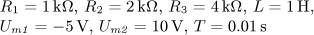
výsledek úloha 7

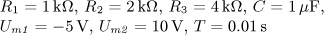
výsledek
úloha 8 
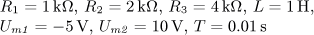
výsledek
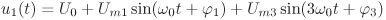
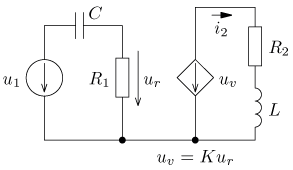
obsahující ideální zdroj napětí řízený napětím
uv = K ur jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního proudu i2(t) a jeho efektivní hodnotu I2.
Vypočítejte činný, jalový, zdánlivý a deformační výkon a účiník výstupní části obvodu.
Návrat na přehled příkladů úloha 1
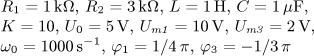
výsledek
úloha 2 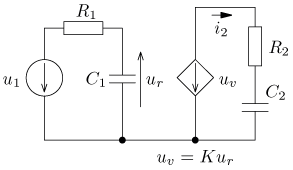
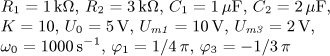
výsledek
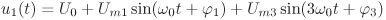
obsahující ideální zdroj napětí řízený proudem
uv = R ir jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního proudu i2(t) a jeho efektivní hodnotu I2.
Vypočítejte činný, jalový, zdánlivý a deformační výkon a účiník výstupní části obvodu.
Návrat na přehled příkladů úloha 1
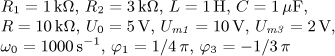
výsledek
úloha 2 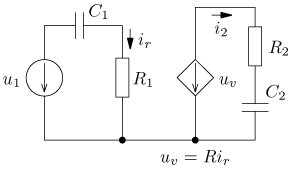
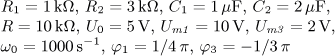
výsledek
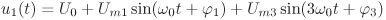
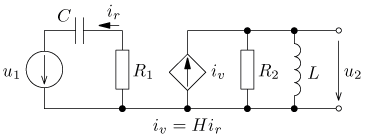
obsahující ideální zdroj proudu řízený proudem
iv = H ir jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního napětí u2(t) a jeho efektivní hodnotu U2.
Vypočítejte činný, jalový, zdánlivý a deformační výkon a účiník výstupní části obvodu.
Návrat na přehled příkladů úloha 1
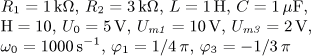
výsledek
úloha 2 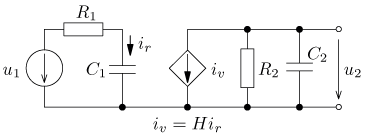
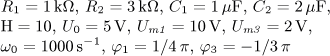
výsledek
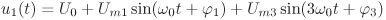
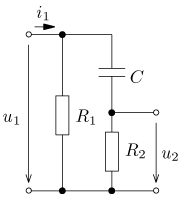
jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního napětí u2(t) a jeho efektivní hodnotu U2.
Vypočítejte činný, jalový, zdánlivý a deformační výkon zdroje a jeho účiník.
Návrat na přehled příkladů úloha 1
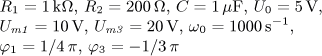
výsledek
úloha 2 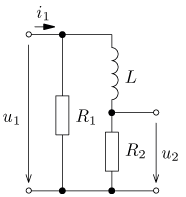
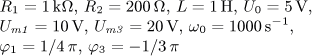
výsledek úloha 3
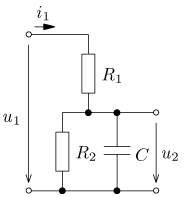
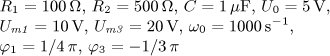
výsledek
úloha 4 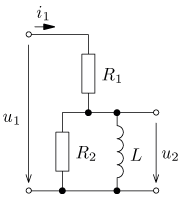
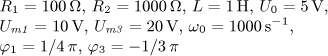
výsledek
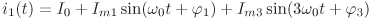
jsou v ustáleném stavu. Vypočítejte časový průběh
výstupního napětí u2(t) a jeho efektivní hodnotu U2.
Vypočítejte činný, jalový, zdánlivý a deformační výkon zdroje a jeho účiník.
Návrat na přehled příkladů úloha 1

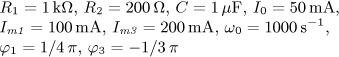
výsledek
úloha 2 
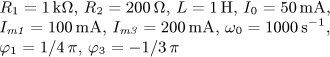
výsledek úloha 3

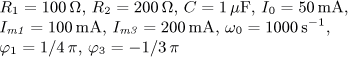
výsledek
úloha 4 
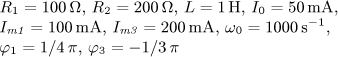
výsledek 
tak, aby žádná z vyšších harmonických složek
(v příkladu při zkoušce vždy pouze jedna z variant)
neměla amplitudu větší než x% amplitudy první harmonické.
Návrat na přehled příkladů obr. 1
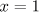
výsledek
obr. 2 
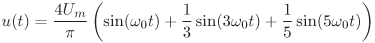
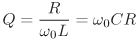
tak, aby žádná z vyšších harmonických složek
(v příkladu při zkoušce vždy pouze jedna z variant)
neměla amplitudu větší než x% amplitudy první harmonické.
Návrat na přehled příkladů obr. 1
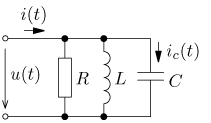
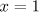
výsledek
obr. 2 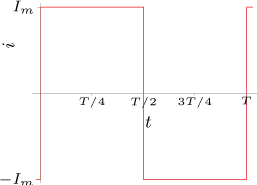
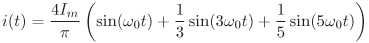
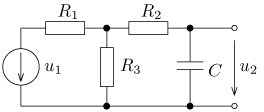
u(t) = U0 + Um1 sin( ω0t)
+ Um2 sin(2 ω0t)
+ Um3 sin(3 ω0t) [V].
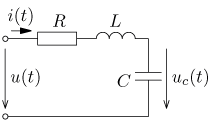
Určete časový
průběh proudu i(t) v ustáleném stavu a činný výkon dodávaný obvodu zdrojem.
Návrat na přehled příkladů obr. 1

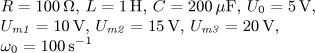
výsledek
i(t) = I0 + Im1 sin( ω0t)
+ Im2 sin(2 ω0t)
+ Im3 sin(3 ω0t) [A].
Určete časový
průběh napětí u(t) v ustáleném stavu a činný výkon dodávaný obvodu zdrojem.
Návrat na přehled příkladů obr. 1

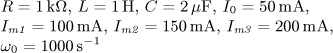
výsledek
Analýza přechodných jevů (v časové oblasti).
(Operátorová) analýza přechodných jevů
Příklady jsou shodné s předchozím tématickým okruhem,
protože v případě řešení přechodných jevů není metoda řešení předepisována
a záleží na volbě studenta.
Obvody s rozprostřenými parametry - bezeztrátové vedení.
Návrat na přehled příkladů úloha 1
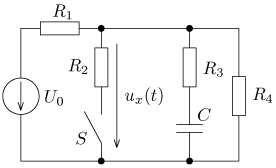
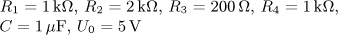
výsledek
úloha 2 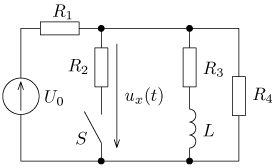
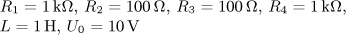
výsledek úloha 3
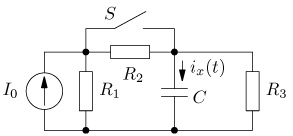
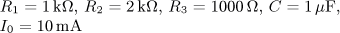
výsledek
úloha 4 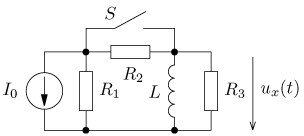
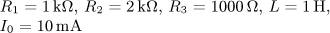
výsledek úloha 5
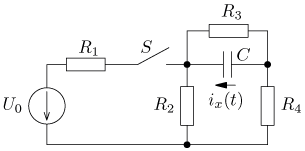
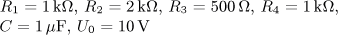
výsledek
úloha 6 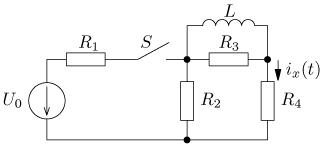
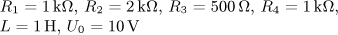
výsledek úloha 7
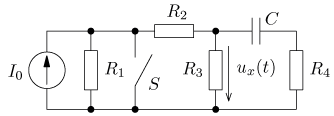
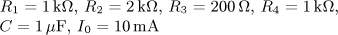
výsledek
úloha 8 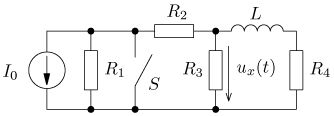
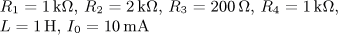
výsledek úloha 9
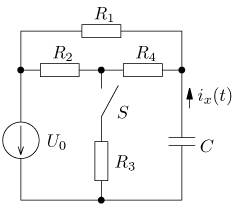
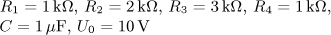
výsledek
úloha 10 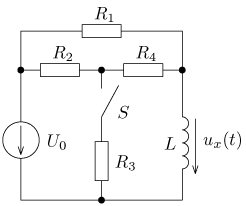
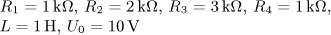
výsledek úloha 11
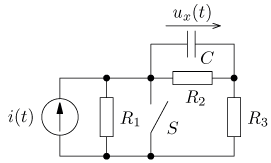
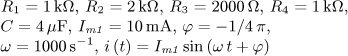
výsledek
úloha 12 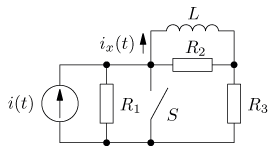
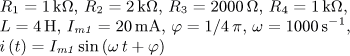
výsledek úloha 13
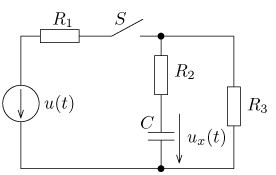
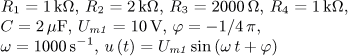
výsledek
úloha 14 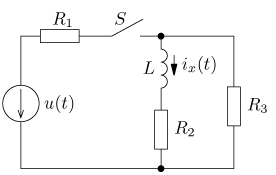
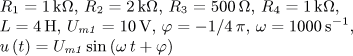
výsledek úloha 15
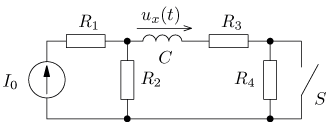
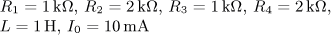
výsledek
Návrat na přehled příkladů úloha 1
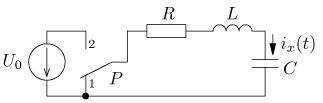
výsledek
Návrat na přehled příkladů úloha 1
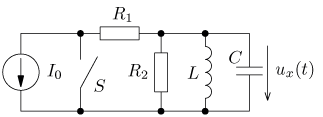
výsledek
Návrat na přehled příkladů úloha 1
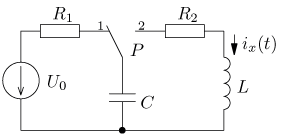
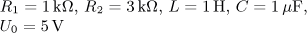
výsledek
úloha 2 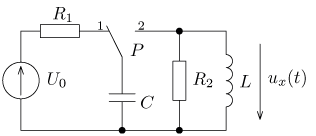
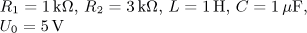
výsledek
Návrat na přehled příkladů úloha 1
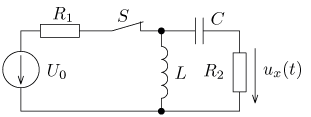
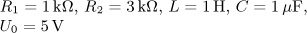
výsledek
úloha 2 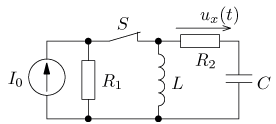
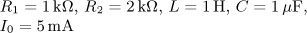
výsledek úloha 3
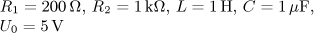
výsledek
úloha 4 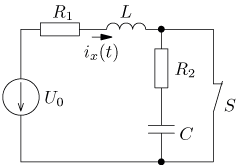
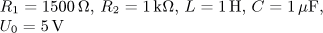
výsledek
Doporučení:Pro řešení použijte Laplaceovu transformaci.
Návrat na přehled příkladů úloha 1
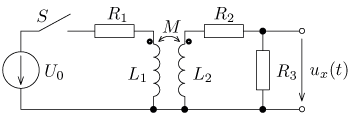
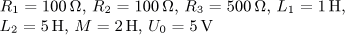
výsledek
Návrat na přehled příkladů
Návrat na přehled příkladů
úloha 1 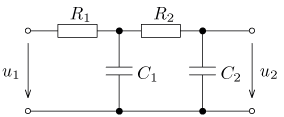
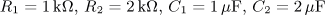
výsledek: P(p), a(t),
w(t)
úloha 2 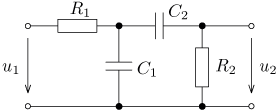
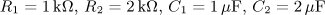
výsledek: P(p), a(t),
w(t)
úloha 3 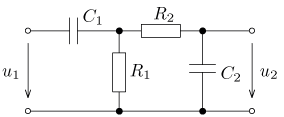
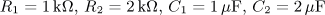
výsledek: P(p), a(t),
w(t)
úloha 4 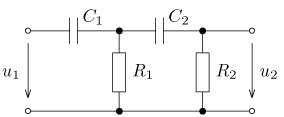
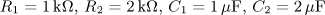
výsledek: P(p), a(t),
w(t)
úloha 5 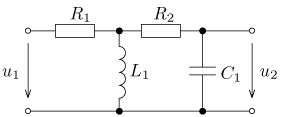
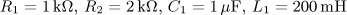
výsledek: P(p), a(t),
w(t)
úloha 6 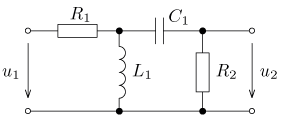
výsledek: P(p), a(t),
w(t)
úloha 7 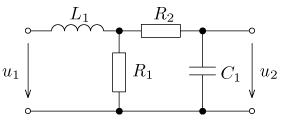
výsledek: P(p), a(t),
w(t)
úloha 8 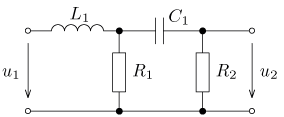
výsledek: P(p), a(t),
w(t)
úloha 9 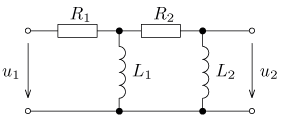
výsledek: P(p), a(t),
w(t)
úloha 10 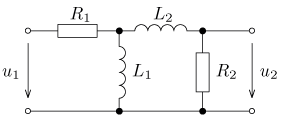
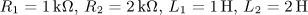
výsledek: P(p), a(t),
w(t)
úloha 11 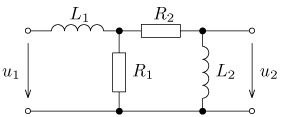
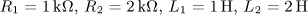
výsledek: P(p), a(t),
w(t)
úloha 12 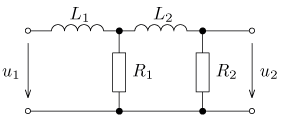
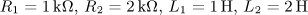
výsledek: P(p), a(t),
w(t)
úloha 13 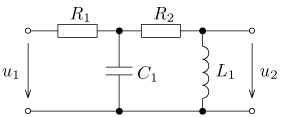
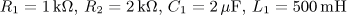
výsledek: P(p), a(t),
w(t)
úloha 14 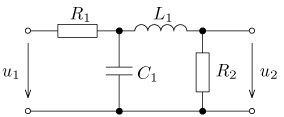
výsledek: P(p), a(t),
w(t)
úloha 15 
výsledek: P(p), a(t),
w(t)
úloha 16 
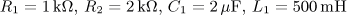
výsledek: P(p), a(t),
w(t)
úloha 17 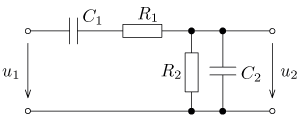
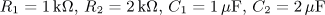
výsledek: P(p), a(t),
w(t)
úloha 18 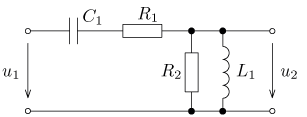
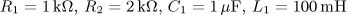
výsledek: P(p), a(t),
w(t)
úloha 19 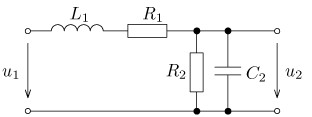
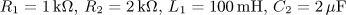
výsledek: P(p), a(t),
w(t)
úloha 20 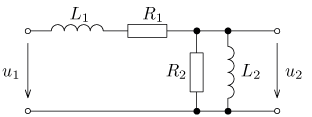
výsledek: P(p), a(t),
w(t)
úloha 21 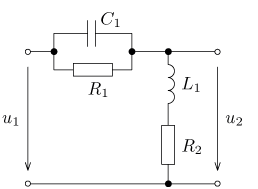
výsledek: P(p), a(t),
w(t)
úloha 22 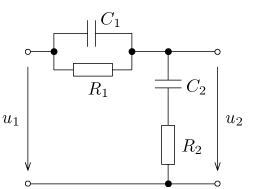
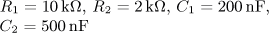
výsledek: P(p), a(t),
w(t)
úloha 23 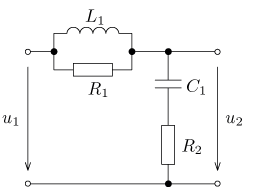
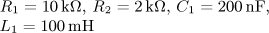
výsledek: P(p), a(t),
w(t)
úloha 24 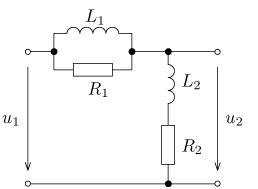
výsledek: P(p), a(t),
w(t)
úloha 25 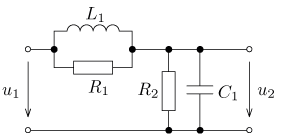
výsledek: P(p), a(t),
w(t)
úloha 26 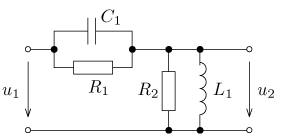
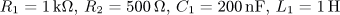
výsledek: P(p), a(t),
w(t)
Návrat na přehled příkladů