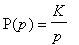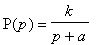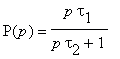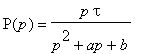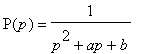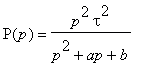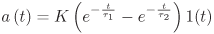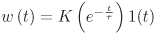Elektrické obvody 2 (X31EO2)
Otázky k procvičení
Otázky jsou k dispozici jako soubor .pdf,
.doc, nebo následují jako "klasická" html stránka.
Přehled otázek:
- Uveďte všechny tvary Fourierovy řady, které znáte.
- Uveďte vztahy pro výpočet koeficientů reálné Fourierovy řady.
- Uveďte vztah pro výpočet koeficientů komplexní Fourierovy řady.
- Definujte efektivní hodnotu periodického průběhu proudu (napětí).
- Uveďte vztah pro výpočet efektivní hodnoty periodického průběhu proudu (napětí) daného Fourierovou řadou.
- Definujte činný výkon periodického neharmonického průběhu napětí a proudu obecného dvojpólu.
- Uveďte vztah pro výpočet činného výkonu periodického neharmonického průběhu napětí a proudu dvojpólu, je-li napětí i proud vyjádřeno Fourierovými řadami.
- Uveďte vztah pro výpočet jalového výkonu periodického neharmonického průběhu napětí a proudu dvojpólu, je-li napětí i proud vyjádřeno Fourierovými řadami.
- Uveďte vztah pro výpočet zdánlivého výkonu periodického neharmonického průběhu napětí a proudu dvojpólu, je-li napětí i proud vyjádřeno Fourierovými řadami.
- Uveďte vztah pro výpočet deformačního výkonu periodického neharmonického průběhu napětí a proudu dvojpólu.
- Popište jak lze dospět k Fourierově transformaci neperiodického signálu zobecněním vztahů pro komplexní Fourierovy řady periodických průběhů.
- Uveďte, pro které typy neperiodických signálů existuje jejich Fourierův obraz.
- Popište postup, kterým lze podstatně rozšířit množinu funkcí transformovatelných Fourierovou transformací pomocí transformace Laplaceovy.
- Uveďte větu o obrazu derivace v Laplaceově transformaci.
- Uveďte větu o obrazu integrálu v Laplaceově transformaci.
- Vyjádřete impedanci lineárního pasivního dvojpólu protékaného harmonickým proudem
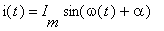 na němž je
v ustáleném stavu harmonické napětí
na němž je
v ustáleném stavu harmonické napětí 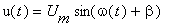 .
.
- Vyjádřete impedanci obecného lineárního pasivního dvojpólu protékaného obecným
průběhem proudu i(t) na němž je napětí u(t), je-li i(t) = 0 pro
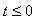 , u(t) = 0
pro
, u(t) = 0
pro 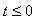 .
.
- Vyjádřete admitanci lineárního pasivního dvojpólu protékaného harmonickým proudem
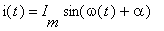 na němž je v ustáleném stavu harmonické napětí
na němž je v ustáleném stavu harmonické napětí
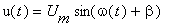 .
.
- Vyjádřete admitanci obecného lineárního pasivního dvojpólu protékaného obecným
průběhem proudu i(t) na němž je napětí u(t), je-li
i(t) = 0 pro
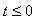 ,
u(t) = 0 pro
,
u(t) = 0 pro 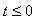 .
.
- Vyjádřete napěťový přenos lineárního pasivního obvodu napájeného zdrojem napětí
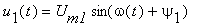 , je-li jeho výstupní napětí
v ustáleném stavu
, je-li jeho výstupní napětí
v ustáleném stavu 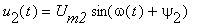 .
.
- Vyjádřete napěťový přenos lineárního pasivního obvodu napájeného zdrojem napětí
u1(t) obecného průběhu, je-li jeho výstupní napětí
u2(t). Předpokládejte, že
u1(t) = 0 pro
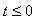 ,
u2(t) = 0 pro
,
u2(t) = 0 pro 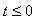 .
.
- Nakreslete sériové náhradní zapojení nabitého kapacitoru tvořené impedancí
a zdrojem počáteční podmínky.
- Nakreslete paralelní náhradní zapojení nabitého kapacitoru tvořené admitancí
a zdrojem počáteční podmínky.
- Nakreslete sériové náhradní zapojení induktoru s počátečním proudem
iL(0+) tvořené impedancí a zdrojem počáteční podmínky.
- Nakreslete paralelní náhradní zapojení induktoru s počátečním proudem
iL(0+) tvořené admitancí a zdrojem počáteční podmínky.
- Uveďte vztahy mezi Laplaceovými obrazy napětí a proudu lineárního rezistoru.
- Uveďte vztahy mezi Laplaceovými obrazy napětí a proudu nabitého kapacitou.
- Uveďte vztahy mezi Laplaceovými obrazy napětí a proudu induktoru s počátečním
proudem iL(0+).
- Lineární obvod je popsán diferenciální rovnicí typu
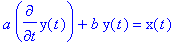 Uveďte obecné řešení této rovnice a jeho modifikaci pro buzení konstantou (stejnosměrné
zdroje) nebo harmonickou funkcí (sinusové zdroje).
Uveďte obecné řešení této rovnice a jeho modifikaci pro buzení konstantou (stejnosměrné
zdroje) nebo harmonickou funkcí (sinusové zdroje).
- Lineární obvod je popsán diferenciální rovnicí typu
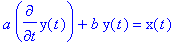 Uveďte obecné řešení této rovnice a jeho modifikaci pro buzení harmonickou funkcí (sinusové
zdroje).
Uveďte obecné řešení této rovnice a jeho modifikaci pro buzení harmonickou funkcí (sinusové
zdroje).
- Lineární obvod je popsán diferenciální rovnicí
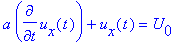 Najděte řešení této rovnice pro obecnou počáteční podmínku ux(0+).
Najděte řešení této rovnice pro obecnou počáteční podmínku ux(0+).
- Lineární obvod je popsán diferenciální rovnicí
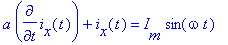 Najděte řešení této rovnice, je-li ix(0) = 0.
Najděte řešení této rovnice, je-li ix(0) = 0.
- Lineární obvod je popsán diferenciální rovnicí
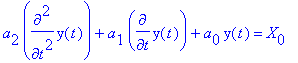 Uveďte obecné řešení této rovnice, má-li charakteristická rovnice dva reálné různé
kořeny
Uveďte obecné řešení této rovnice, má-li charakteristická rovnice dva reálné různé
kořeny 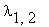 , X0 = konst.
, X0 = konst.
- Lineární obvod je popsán diferenciální rovnicí
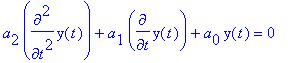 Uveďte obecné řešení této rovnice, má-li charakteristická rovnice jeden dvojnásobný
kořen
Uveďte obecné řešení této rovnice, má-li charakteristická rovnice jeden dvojnásobný
kořen 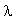 .
.
- Lineární obvod je popsán diferenciální rovnicí
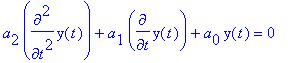 Uveďte obecné řešení této rovnice, má-li charakteristická rovnice dvojici komplexních
kořenů
Uveďte obecné řešení této rovnice, má-li charakteristická rovnice dvojici komplexních
kořenů 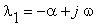 ;
;
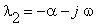 .
.
- Pro lineární obvod obsahující m neslučitelných kapacitorů a n neslučitelných
induktorů popište rozdíl mezi energetickými a matematickými počátečními podmínkami.
- Uveďte fyzikální význam přechodové charakteristiky lineárního obvodu.
- Vyjádřete obecně přechodovou charakteristiku lineárního obvodu jehož vstupní veličinou
je x1(t) a výstupní veličinou x2(t).
- Vyjádřete přechodovou charakteristiku lineárního obvodu se vstupní veličinou
u1(t) a výstupní veličinou u2(t) a uveďte možnosti jejího změření.
- Vyjádřete obecně impulzní charakteristiku lineárního obvodu jehož vstupní veličinou
je x1(t) a výstupní veličinou x2(t).
- Popište impulzní charakteristiku lineárního obvodu se vstupní veličinou
u1(t) a výstupní veličinou u2(t) a uveďte možnosti jejího změření.
- Jakou podmínku musí splňovat póly přenosové funkce, aby byla impulzní charakteristika
ohraničenou funkcí (stabilní obvod)?
- Uveďte z jakých složek (typů funkcí) se může skládat impulzní charakteristika
stabilního obvodu se soustředěnými parametry.
- Udejte vztah mezi přechodovou a impulsní charakteristikou téhož obvodu.
- Pro obvod s přenosem P(p) = U2(p)/U1(p) uveďte obecné vztahy
pro výpočet modulové a fázové frekvenční charakteristiky (vyjádření veličin na svislých
osách uvedených charakteristik).
- Pro obvod s přenosem
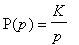 nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
- Pro obvod s přenosem
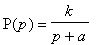 nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
- Pro obvod s přenosem
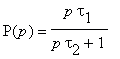 nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
nakreslete asymptotické
vyjádření modulové a fázové frekvenční charakteristiky v logaritmických souřadnicích.
- Pro obvod s přenosem
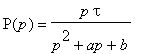 nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li
přenos 2 reálné záporné póly p1, p2.
nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li
přenos 2 reálné záporné póly p1, p2.
- Pro obvod s přenosem
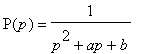 nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li přenos
2 reálné záporné póly p1, p2.
nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li přenos
2 reálné záporné póly p1, p2.
- Pro obvod s přenosem
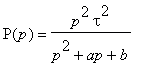 nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li přenos
2 reálné záporné póly p1, p2.
nakreslete asymptotické
vyjádření modulové frekvenční charakteristiky v logaritmických souřadnicích, má-li přenos
2 reálné záporné póly p1, p2.
- Pro obvod, jehož přechodová charakteristika je
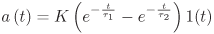 nakreslete asymptotické vyjádření modulové frekvenční charakteristiky v logaritmických
souřadnicích.
nakreslete asymptotické vyjádření modulové frekvenční charakteristiky v logaritmických
souřadnicích.
- Pro obvod, jehož impulzní charakteristika je
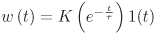 nakreslete asymptotické vyjádření modulové a fázové frekvenční charakteristiky
v logaritmických souřadnicích.
nakreslete asymptotické vyjádření modulové a fázové frekvenční charakteristiky
v logaritmických souřadnicích.
- Určete obecně výstupní napětí obvodu popsaného pro napěťový přenos impulzní
charakteristikou w(t), je-li dáno vstupní napětí u1(t).
- Určete obecně výstupní napětí obvodu popsaného pro napěťový přenos přechodovou
charakteristikou a(t), je-li vstupní napětí
u1(t) = Um 1(t) - Um 1(t-t0).
(Obdélníkový impulz délky t0).
- Nakreslete náhradní schéma elementu bezeztrátového vedení a odvoďte jeho základní
rovnice.
- Napište vlnovou rovnici homogenního bezeztrátového vedení a uveďte její řešení.
- Dokažte, že libovolné funkce typu
u(x,t) = f1(x-vt) + f2(x+vt)
jsou řešením vlnové rovnice pro homogenní bezeztrátové vedení.
- Uveďte vztahy pro výpočet vlnového odporu a rychlosti šíření vln na homogenním bezetrátovém vedení při znalosti primárních parametrů vedení na jednotku délky ( L a C).
- Definujte činitel odrazu vln na styku dvou vedení s různými vlnovými odpory a udejte vztah pro jeho velikost.
- Definujte činitel prostupu vln na styku dvou vedení s různými vlnovými odpory a udejte vztah pro jeho velikost.
- Určete činitele odrazu na konci bezeztrátového vedení zakončeného naprázdno a nakrátko.
- Určete činitele odrazu na konci bezetrátového vedení zakončeného odporem Rs
rovným vlnovému odporu R0.
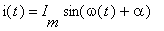 na němž je
v ustáleném stavu harmonické napětí
na němž je
v ustáleném stavu harmonické napětí 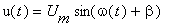 .
.
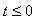 , u(t) = 0
pro
, u(t) = 0
pro 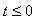 .
.
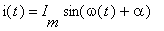 na němž je v ustáleném stavu harmonické napětí
na němž je v ustáleném stavu harmonické napětí
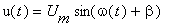 .
.
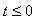 ,
u(t) = 0 pro
,
u(t) = 0 pro 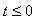 .
.
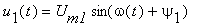 , je-li jeho výstupní napětí
v ustáleném stavu
, je-li jeho výstupní napětí
v ustáleném stavu 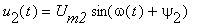 .
.
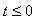 ,
u2(t) = 0 pro
,
u2(t) = 0 pro 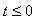 .
.
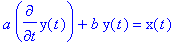
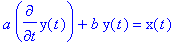
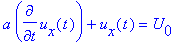
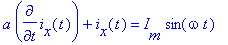
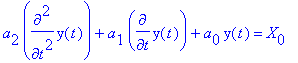
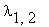 , X0 = konst.
, X0 = konst.
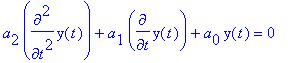
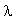 .
.
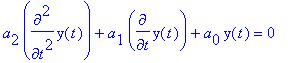
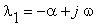 ;
;
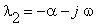 .
.
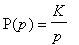
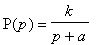
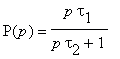
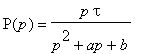
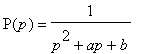
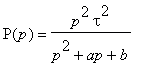
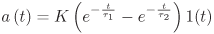
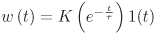
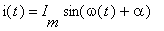 na němž je
v ustáleném stavu harmonické napětí
na němž je
v ustáleném stavu harmonické napětí 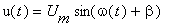 .
.
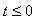 , u(t) = 0
pro
, u(t) = 0
pro 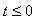 .
.
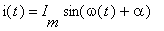 na němž je v ustáleném stavu harmonické napětí
na němž je v ustáleném stavu harmonické napětí
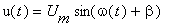 .
.
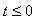 ,
u(t) = 0 pro
,
u(t) = 0 pro 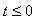 .
.
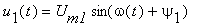 , je-li jeho výstupní napětí
v ustáleném stavu
, je-li jeho výstupní napětí
v ustáleném stavu 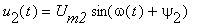 .
.
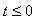 ,
u2(t) = 0 pro
,
u2(t) = 0 pro 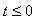 .
.
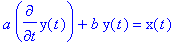
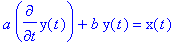
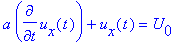
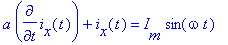
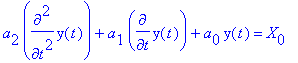
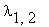 , X0 = konst.
, X0 = konst.
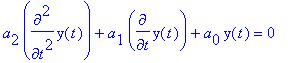
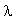 .
.
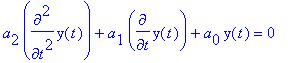
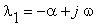 ;
;
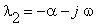 .
.