aeo_zzv.html

Ananlýza zpětnovazební soustavy

soubor pro MAPLE 6

> restart;

Nejdříve načteme potřebné knihovny.

> with(Syrup):with(plots):

Warning, the name changecoords has been redefined

Budeme analyzovat vliv záporné zpětné vazby (ZZV) na některé vlastnosti soustavy, která obsahuje zesilovač se dvěma póly a odporovou zápornou zpětnou vazbu (ZZV) podle následujícího obrázku. Pro další analýzy budeme potřebovat jednak přenos celkového zapojení (se ZV) - a jednak přenos otevřené zpětnovazevbní smyčky - .

Zadání soustav pro analýzu

První pól zesilovače je zadán obecně, další dva jsou na 2MHz a 4MHz. Zpětnovazební odpor je také zadán obecně (bez numerické hodnoty). Ostatní prvky jsou zadány s numerickými hodnotami.

> ZZ:= "invertující zesilovač
V 1 0
R01 1 2 10E3
Rp1 2 3
Rz1 3 0 10E3
Rp2 4 5
Rz2 4 0 10E3
R02 5 0 10E3
Ra2 5 0 100E3
X1 2 3 0 zesilovac
X2 1 4 0 zesilovac
.subckt zesilovac a b c
Ra a c 100E3
Ri d b 10
E1 d c a c -500/(1+s/(2*Pi*1.6E3))/(1+s/(2*Pi*16E3))
.ends
.end":

Analýza systému pro a

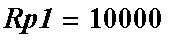
Analýza a výpočet napěťového přenosu zesilovače se ZV a otevřené ZV smyčky.

> napeti:=syrup(ZZ, ac):

> Pzv:=simplify(subs(napeti,v[3]/v[1])):

> Pos:=simplify(subs(napeti,v[5]/v[1])):

Syrup/parsedeck:   Analyzing SPICE deck "invertující zesilovač" (ignoring this line)

Modulová charakteristika zesilovače pro a (zesilení přibližně 1).

> modul:=simplify(evalc(abs(subs({Rp1=10E3,s=I*omega},Pzv)))):

> semilogplot(20*log10(modul),omega=1E3..1E7,title=`MODUL`);

Výpočet vratného rozdílu pro stejnosměrný (ss) signál a

> F:=subs(s=0,1-Pos):

> evalf(subs(Rp2=10e3,F));

Výpočet zesílení pro ss signál a a pro systém bez ZV (nezakončeno => nevyjde A/F hlavně díky K1).

> evalf(subs({s=0,Rp1=10e3},Pzv));

> evalf(subs(s=0,limit(Pzv,Rp1=infinity)));

Následuje výpočet pólů přenosu pro zadaný systém (se ZV).

> sol1:=solve(denom(subs(Rp1=10E3,Pzv)));

Skutečnost, že je systém nestabilní lze také jednoduše určit Laplaceovou transformací přenosu (impulzní charakteristikou).

> with(inttrans);

Impulzní charakteristika obsahuje i Diracův impulz, protože výstupní odpor zesilovače není nulový (není nulvový přenos K3). Jelikož jsou póly komplexní, musí být odezva kmitavý charakter (tlumený harmonický průběh) a úhlový kmitočet oscilací se správně rovná imag. hodnotě kořenů jmenovatele přenosu (vyšlo).

> odezva:=simplify(invlaplace(subs(Rp1=10E3,Pzv),s,t));

Že je násobná konstanta skutečně koeficientem K3 se lze přesvědčit jednoduchým výpočtem.

> K3:=Ra/(R0+Ra)*Ri*Rz/(Ri+Rz)/(R0*Ra/(R0+Ra)+Rp+Ri*Rz/(Ri+Rz));
evalf(subs({Ra=100E3,R0=10E3,Rp=10E3,Ri=10,Rz=10E3},%));

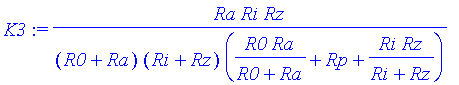
Takto pak vypadá impulzní charakteristika. Musí se samozřejmě jednat o stabilní systém (systém pouze se ZZV a dvěma póly přenosu).

> plot(odezva,t=1E-10..1E-4, title=`Impulzni charakteristika`);

Výpočet hodnoty odporu pro maximálně plochou modulovou charakteristiku

V předešlém případě byl analyzován systém s , kde modulová charakteristika vykazovala výrazný překmit. Nyní vypočtěme hodnotu zpětnovazebního odporu tak, aby modulová chrakteristika byla právě maximálně plochá, tj. reálná i imaganární část kořenů se sobě rovnala.

Výpočet kořenů obecně:

> koreny:=solve(denom(Pzv),s);

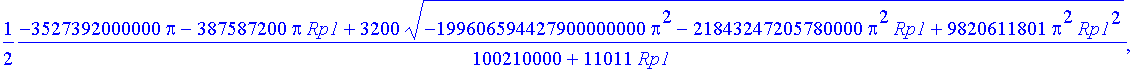
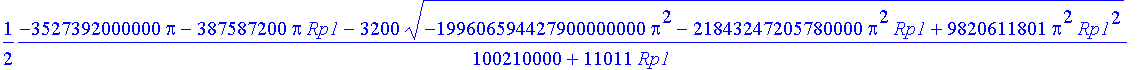
Toto samotné nevede k vyjádření reálné části.

> Re(koreny[1]);

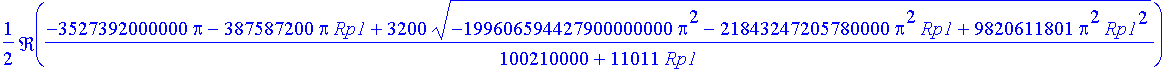
Toto už ano.

> evalc(Re(koreny[1]));

Musíme porovnávat absolutní hodnoty jednotlivých částí, jelikož nezáleží na znaménku, ale na velikosti.

> Rpp:=solve(evalc(abs(Re(koreny[1])))=evalc(abs(Im(koreny[1]))),Rp1);

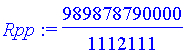
> evalf(Rpp);

Vykreslení modulových charakreristik pro (maximálně plochá charakteristika), pro a .

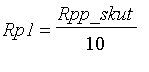> modul1:=simplify(evalc(abs(subs({Rp1=Rpp/10,s=I*omega},Pzv)))):

> modul2:=simplify(evalc(abs(subs({Rp1=Rpp,s=I*omega},Pzv)))):

> modul3:=simplify(evalc(abs(subs({Rp1=Rpp*10,s=I*omega},Pzv)))):

> i:=semilogplot(20*log10(modul1),omega=1E3..1E6,title=`MODUL`,color=green):

> j:=semilogplot(20*log10(modul2),omega=1E3..1E6,title=`MODUL`,color=red):

> k:=semilogplot(20*log10(modul3),omega=1E3..1E6,title=`MODUL`,color=blue,numpoints=200):

> display(i,j,k);

Závislost polohy pólů zesilovače na vlivu ZV (hodnotě 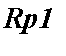, resp. vratného rozdílu )

Výpočet pólů přenosu systému se ZV pro 3 různé hodnoty zpětnovazebího odporu ( ).

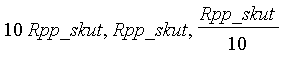> poly:=seq([solve(denom(subs(Rp1=R0,Pzv)),s)],R0=[Rpp*10,Rpp,Rpp/10]);

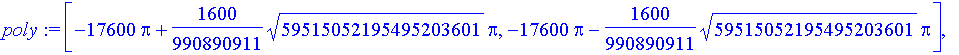
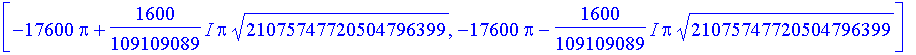
> barva:=[blue,red,green];

Vykreslení pólů. Je nutné sledovat póly podle barev. Stejné barvy = stejná hodnota , resp. vratného rozdílu .

> for i from 1 to 3 do
graf[i]:=complexplot(poly[i], Re=-1e5..0, style=point, title=`Poloha pólů přenosu ZV soustavy v závislosti na Rp`,color=barva[i]);
od:
display(graf[1],graf[2],graf[3]);

Vykreslení pólů pro větší rozsah zpětnovazebního odporu.

> vv:=seq(fsolve(denom(subs({Rp1=10^(R0/4)},Pzv)),s,complex),R0=1..30):complexplot([vv], Re=-1e5..0, style=point, title=`Poloha pólů přenosu ZV soustavy v závislosti na Rp`);

Porování kmitočtových závislostí přenosu invertujícího a neinvertujícího kompenzovaného zesilovače - vliv členu alpha na kmitočtovou závislost přenosu

Zadání prakticky stejného sesilovače jako v předchozím případě, s tím rozdílem, že je neinvertující, viz. obr.

> ZZ1:= "neinvertující zesilovač
V 1 0
R01 2 0 10E3
Rp1 2 3
Rz1 3 0 10E3
X1 1 2 3 0 zesilovac
.subckt zesilovac a b c d
Ra a b 100E3
Ri e c 10
E1 e d a b 500/(1+s/(2*Pi*1.6E3))/(1+s/(2*Pi*16E3))
.ends
.end":

Analýza a výpočet napěťového přenosu.

> napetiI:=syrup(ZZ1, ac):

> PzvI:=simplify(subs(napetiI,v[3]/v[1])):

Syrup/parsedeck:   Analyzing SPICE deck "neinvertující zesilovač" (ignoring this line)

Aby měl zesilovač zesílení rovno -1, je nutné zapojit do ZV invertujícího zesilovače odpor , do ZV neinvertujícího zesilovače odpor . Následuje výpočet těchto odporů.

> Rp1_1:=evalf(solve(subs(s=0,Pzv)=-1));

> Rp1_1I:=evalf(solve(subs(s=0,PzvI)=1));

nemůže vyjít nulový díky nenuovému výst. odporu zesilovače.

Vykreslení modulových charakteristik neinvertujícího zesilovače "bez ZV" (není korektně zakončeno, ale chyba zde nebude patrná), neinvertujícího a invertujícího zesilovače s napěťovým přenosem 1. Invertující zesilovač s patrným rozdílem především díky rozdílnému členu .

> modul1I:=simplify(evalc(abs(subs(s=I*omega,limit(Pzv1,Rp1=infinity))))):

> modul2I:=simplify(evalc(abs(subs({Rp1=Rp1_1,s=I*omega},Pzv)))):

> modul3I:=simplify(evalc(abs(subs({Rp1=Rp1_1I,s=I*omega},PzvI)))):

> semilogplot([20*log10(modul1I),20*log10(modul2I),20*log10(modul3I)],omega=1E4..1E7,title=`MODUL`,color=[red,green,blue],numpoints=200);

Lze ještě další vlivy (na kmit. vlastnosti - dodělat, na změnu zesílení)