![[Maple Bitmap]](images_ft/ft1.gif)
![[Maple Bitmap]](images_ft/ft2.gif)
Fourierova transformace a její souvislost Fourierovou řadou
© Jiří Hospodka
Následující ukázka demonstroje použití programu Maple pro podporu výuky Fourierovy transformace v předmětech Elektrické obvody 2 (EO2) a počítačové řešení elektrických obvodů (PRO).
![[Maple Bitmap]](images_ft/ft1.gif)
![[Maple Bitmap]](images_ft/ft2.gif)
Vyjděme z Fourierovy řady uvedeného periodického signálu a pokusme se odtud přejít k Fourierovu obrazu uvedeného obdélníkového pulzu. Většina operací je zatím bez komentáře (ty lze slyšet na cvičení :-).
Fourierova řada obdélníkového signálu podle obrázku, závistost spektrélních čar na parametech signálu
| > | f:=(t,t0::Range(0,0.5))->signum(cos(2*Pi*t)-cos(2*Pi*t0))/2+1/2; |
![]()
| > | rect:=plot(f(t,1/16),t=-0.5..2.5,color=blue): |
| > | rect; |
![[Maple Plot]](images_ft/ft4.gif)
| > | ck:=1/T*int(A*exp(-I*k*omega0*t),t=-tau/2..tau/2); |
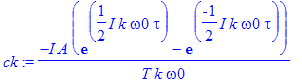
| > | ck:=simplify(ck); |
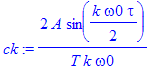
| > | ckn:=subs(A=1,tau=T/8,omega0=2*Pi/T,ck); |
| > | ck0:=limit(ckn,k=0); |
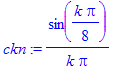
![]()
| > | sinx:=plot(1/8*sin(Pi*k/8)/(Pi*k/8),k=-20..20,color=blue): |
| > | sinx8:=plot([seq([[k,0],[k,ckn]],k=-20..-1),[[0,0],[0,ck0]],seq([[k,0],[k,ckn]],k=1..20)],color=red,thickness=3,xtickmarks=20): |
| > | plots[display](sinx,sinx8); |
![[Maple Plot]](images_ft/ft9.gif)
| > | limit(sin(x)/x,x=0); |
![]()
Vztah ck lze upravit na tvar
![[Maple Bitmap]](images_ft/ft11.gif)
x
![[Maple Bitmap]](images_ft/ft12.gif)
Kontrola
| > | temp:=simplify(sum(ckn*exp(I*k*2*Pi*t),k=-10..-1)+ck0+sum(ckn*exp(I*k*2*Pi*t),k=1..10)): |
| > | pt:=plot(temp,t=-0.3..2.3,thickness=3,numpoints=200): |
| > | plots[display](pt,rect); |
![[Maple Plot]](images_ft/ft13.gif)
| > |
Změna periody T
Dosaďme nyní za
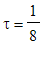 ,
,
![]() a měňme periodu T od 1 do 5 s.
a měňme periodu T od 1 do 5 s.
| > | ckn:=subs(A=1,tau=1/8,omega0=2*Pi/T,ck): |
| > | ck0:=limit(ckn,k=0): |
| > | plots[animate](plot,[[seq([[k/T,0],[k/T,ckn]],k=-100..-1),[[0,0],[0,ck0]],seq([[k/T,0],[k/T,ckn]],k=1..100)],color=red,thickness=3,xtickmarks=20,view=[-20..20, 0.13..-0.03]],T=[1,2,3,4,5]); |
![[Maple Plot]](images_ft/ft16.gif)
| > |
Změna periody T pro součin ck*T
| > | ck*T; |
| > | ckn:=subs(A=1,tau=1/8,omega0=2*Pi/T,T*ck): |
| > | ck0:=limit(ckn,k=0): |
| > | plots[animate](plot,[[seq([[k/T,0],[k/T,ckn]],k=-100..-1),[[0,0],[0,ck0]],seq([[k/T,0],[k/T,ckn]],k=1..100)],color=red,thickness=3,xtickmarks=20,view=[-20..20, 0.13..-0.03]],T=[1,2,3,4,5]); |
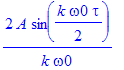
![[Maple Plot]](images_ft/ft18.gif)
| > |
Změna šířky pulzu
![]() pro součin ck*T
pro součin ck*T
| > | cki:=subs(T=5,subs(A=1,tau=1/i,omega0=2*Pi/T,T*ck)); |
| > | ck0:=limit(cki,k=0): |
| > | plots[animate](plot,[[seq([[k/5,0],[k/5,cki]],k=-100..-1),[[0,0],[0,ck0]],seq([[k/5,0],[k/5,cki]],k=1..100)],color=red,thickness=3,xtickmarks=20],i=[6,8,10,20,50,100]); |
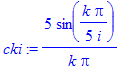
![[Maple Plot]](images_ft/ft21.gif)
| > |
Změna šířky pulzu
![]() pro součin ck*T při konstantní ploše pulzu
pro součin ck*T při konstantní ploše pulzu
![]() *A
*A
| > | cki:=subs(T=5,subs(A=1*i,tau=1/i,omega0=2*Pi/T,T*ck)); |
| > | ck0:=limit(cki,k=0): |
| > | plots[animate](plot,[[seq([[k/5,0],[k/5,cki]],k=-100..-1),[[0,0],[0,ck0]],seq([[k/5,0],[k/5,cki]],k=1..100)],color=red,thickness=3,xtickmarks=20],i=[6,8,10,20,50,100]); |
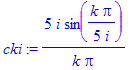
![[Maple Plot]](images_ft/ft25.gif)
| > |
Porovnejme výrazy pro koeficienty komplexní Fourierovy řady a Fourierovu transformaci
| > | ![c[k] = ('1/T')*Int(f(t)*exp(-j*k*omega[0]*t),t = -T/2 .. T/2)](images_ft/ft26.gif)
|
| > | 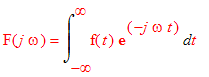
|
Zjistíme, že, ....
Exponenciální tvar
| > | ![f(t) = Sum(c[k]*exp(j*k*omega[0]*t),k = -infinity .. infinity)](images_ft/ft28.gif)
|
Zpětná Fourierova transformace
| > | 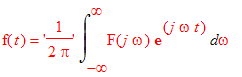
|
Z předchozího je také evidentní, že Fourierův obraz Diracova pulzu je roven jeho ploše.
| > | int(Dirac(t)*exp(-j*omega*t),t =-infinity..infinity); |
Plocha Diracova pulzu.
| > | int(Dirac(t),t=-infinity..infinity); |
![]()
![]()
| > |
Fourierova transformace pulzu
| > | rect:=A*(Heaviside(t+tau/2)-Heaviside(t-tau/2)); |
![]()
| > |
Jednotková funkce
| > | plot(Heaviside(t),t=-1..1,thickness=2); |
![[Maple Plot]](images_ft/ft33.gif)
| > | plot(subs(A=1,tau=1/4,rect),t=-1..1,thickness=2); |
![[Maple Plot]](images_ft/ft34.gif)
| > | int(A*exp(-I*omega*t),t=-tau/2..tau/2); |
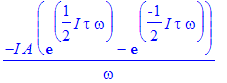
| > | F_rec:=simplify(%); |
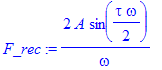
| > | with(inttrans); |
![]()
| > | fourier(rect,t,omega); |
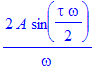
Jak bylo uvedeno, Fourierův obraz Diracova pulzu je roven jeho ploše. Nyní použijme pro výpočet přímý příkaz.
| > | fourier(Dirac(t),t,omega); |
![]()
| > |
Nepoužívat funkci piecewise
| > | rc:=piecewise(t>-tau/2 and t<tau/2,A); |
![rc := PIECEWISE([A, -1/2*tau < t and t < 1/2*tau],[0, otherwise])](images_ft/ft40.gif)
| > | plot(subs(A=1,tau=1/4,rc),t=-1..1,thickness=2); |
![[Maple Plot]](images_ft/ft41.gif)
| > | fourier(rc,t,omega); |
![fourier(PIECEWISE([A, -1/2*tau < t and t < 1/2*tau],[0, otherwise]),t,omega)](images_ft/ft42.gif)
| > |
Fourierova transformace periodických funkcí a vztah mezi Fourierovou tranzformací a řadou
Výsledkem Fourierova obrazu je tedy spojitá funkce, narozdíl od Fourierovy řady. Další odlišností je fyzikální rozměr této funkce (obrazu) oproti fyzikálnímu rozměru koeficientů řady (viz komentář dále). Pro náš případ obdélníhového puzlu dostaneme tedy velmi podobný výraz jeho obrazu v porovnání se vztahem pro fourierovy koeficienty periodicky se opakujícího průběhu. Stejný vztah dostaneme, pokud ve Fourierově obrazu přejdeme od spojitého kmitočtového spektra k diskrétnímu (
![]() ->
->
![]() ) a ten pak dělíme základní periodou signálu.
) a ten pak dělíme základní periodou signálu.
| > | F_rec; |
| > | subs(omega=k*omega0,F_rec)/T; |
| > | ck; |
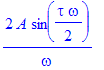
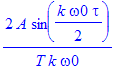
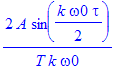
Obecně tedy platí následující pravidlo: Pokud známe Fourierův obraz časově omezené funkce s dobou trvání
![]() , můžeme jednoduše určit koeficienty Fourierovy řady periodické funkce, která vznikla z původní funkce jejím periodickým opakováním s periodou
, můžeme jednoduše určit koeficienty Fourierovy řady periodické funkce, která vznikla z původní funkce jejím periodickým opakováním s periodou
![]() . Tyto koeficienty
. Tyto koeficienty
![]() určíme tak, že do Fourierova obrazu dosadíme
určíme tak, že do Fourierova obrazu dosadíme
![]() (přejdeme od spojitého kmitočtového spektra k diskrétnímu, kde
(přejdeme od spojitého kmitočtového spektra k diskrétnímu, kde
![omega[0] = 2*Pi/T](images_ft/ft52.gif) ) a výsledek pak dělíme periodou
) a výsledek pak dělíme periodou
![]() . To také vyplývá z výše uvedených vztahů - ze vztahu pro koeficienty Fourierovy řady
. To také vyplývá z výše uvedených vztahů - ze vztahu pro koeficienty Fourierovy řady
![]() a pro Fourierův obraz
a pro Fourierův obraz
![]() .
.
Použijme toto pravidlo na náš případ. Mějme symetrický pulz o šířce
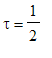 . ...
. ...
| > | plot(subs(A=1,tau=1/2,rect),t=-1..1,thickness=2); |
| > | F_obd:=fourier(rect,t,omega); |
![[Maple Plot]](images_ft/ft57.gif)
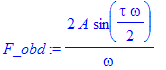
| > | F_obd:=fourier(rect,t,omega); |
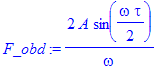
| > | plot(signum(cos(2*Pi*t)),t=0..1.5,thickness=2); |
| > | a_obd:=8/T*int(1*cos(k*2*Pi/T*t), t=0..T/4 ); |
![[Maple Plot]](images_ft/ft60.gif)
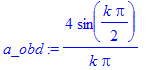
| > | ck:=subs(A=2,omega=k*2*Pi/(tau*2),F_rec)/(2*tau); |
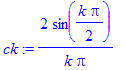
| > | c0:=limit(ck,k=0); |
![]()
| > | evalc(c0+sum(ck*exp(I*2*Pi*k*t),k=-10..-1)+sum(ck*exp(I*2*Pi*k*t),k=1..10)); |
![]()
| > | sum(a_obd*cos(2*Pi*k*t),k=1..10); |
![]()
| > |
| > | fourier(A*exp(I*omega0*t),t,omega) assuming omega0>0; |
| > | fourier(A*cos(omega0*t),t,omega) assuming omega0>0; |
| > | fourier(A*sin(omega0*t),t,omega) assuming omega0>0; |
![]()
![]()
![]()
Tyto vztahy lze poměrně snadno odvodit při znalosti spektra konstantního signálu (
![]() , což lzde dokázat zpětnou fransformací
, což lzde dokázat zpětnou fransformací
![]() ) a použitím věty o kmitočtovém posunu
) a použitím věty o kmitočtovém posunu
![]()
Lze tak získat obraz komplexní exponencialy.
![]() což lze potvrdit zpětnou transformací
což lze potvrdit zpětnou transformací
![]()
Odtud již lze napsat i ostatní vztahy (pro funkce sin a cos), pokud uvážíme, že
![]() . Podobně odvodit i vztah pro obecný periodický signál
. Podobně odvodit i vztah pro obecný periodický signál
![]() kde
kde
![]()
Jaký je tedy vztah mezi spektrem periodického signálu vypočteným pomocí Fourierovy transformace a koeficienty jeho Fourierova rozvoje. Například pro spektrum funkce
![]() platí výše uvedený vztah. Vzhledem k~tomu, že
platí výše uvedený vztah. Vzhledem k~tomu, že
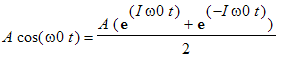 , jsou koeficienty komplexní Fourierovy řady
, jsou koeficienty komplexní Fourierovy řady
![]() =
=
![]() . Jejich grafické znázornění je uvedeno na následijícím obrázku (a). Oproti tomu spektrum stejného signálu
. Jejich grafické znázornění je uvedeno na následijícím obrázku (a). Oproti tomu spektrum stejného signálu
![]() , získané Fourierovou transformací tvoří dva Diracovy pulzy s plochou
, získané Fourierovou transformací tvoří dva Diracovy pulzy s plochou
![]() na kmitočtech
na kmitočtech
![]() a
a
![]() , jak ukazuje obrázek (b).
, jak ukazuje obrázek (b).
![[Maple Bitmap]](images_ft/ft85.gif)
Plocha Diracových pulzů je přitom úměrná velikosti koeficientu
![]() Fourierova rozvoje. Je-li fyzikální rozměr amplitudy
Fourierova rozvoje. Je-li fyzikální rozměr amplitudy
![]() např. [V], pak plocha tohoto pulzu má fyzikální rozměr [V * s * rad / s]=[V * rad]. Pokud tedy chceme znát velikost příslušného koeficientu
např. [V], pak plocha tohoto pulzu má fyzikální rozměr [V * s * rad / s]=[V * rad]. Pokud tedy chceme znát velikost příslušného koeficientu
![]() stačí vydělit plochu odpovídajícího Diracova pulzu členem
stačí vydělit plochu odpovídajícího Diracova pulzu členem
![]() . To také evidentní ze vztahu pro zpětnou Fourierovu transformaci. Pokud ho budeme aplikovat na dané spektrum (např. kosinusového signálu), vynásobené amplitudou
. To také evidentní ze vztahu pro zpětnou Fourierovu transformaci. Pokud ho budeme aplikovat na dané spektrum (např. kosinusového signálu), vynásobené amplitudou
![]() , dostaneme člen
, dostaneme člen
![]() násobený integrálem, udávajícím plochy obou pulzů násobené komplexními exponenciálami, tj.
násobený integrálem, udávajícím plochy obou pulzů násobené komplexními exponenciálami, tj.
![]()
![]()
Po úpravě samozřejmě dostaneme původní signál se správnou velikostí amplitudy.
| > |
Fourierova transformace trojůhelníkového pulzu
| > | troj:=piecewise(t>-t0 and t<=0,(t+t0)/t0*U,t>0 and t<t0,(t0-t)/t0*U,0); |
![troj := PIECEWISE([(t+t0)/t0*U, -t0 < t and t <= 0],[(t0-t)/t0*U, 0 < t and t < t0],[0, otherwise])](images_ft/ft94.gif)
| > | plot(subs(t0=1,U=2,troj),t=-2..2,thickness=2); |
![[Maple Plot]](images_ft/ft95.gif)
| > | F:=int(troj*exp(-I*omega*t),t=-infinity..infinity) assuming t0>0; |
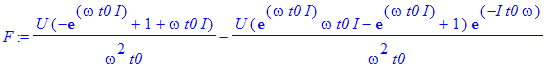
| > | Fu:=simplify(F); |
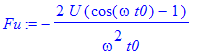
| > | fourier(subs(t0=1,U=2,troj),t,omega);combine(%); |
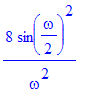
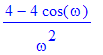
| > | simplify(subs(t0=1,U=2,Fu)); |
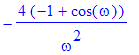
| > | plot(subs(t0=1,U=2,Fu),omega=-4*Pi..4*Pi,thickness=2); |
![[Maple Plot]](images_ft/ft101.gif)
| > | ft:=invfourier(Fu,omega,t) assuming t0>0; |
![]()
| > | convert(ft,piecewise,t) assuming t0>0; |
![PIECEWISE([0, t < -t0],[U/t0*undefined, t = -t0],[(t+t0)/t0*U, t < 0],[U/t0*(t0+undefined), t = 0],[(t0-t)/t0*U, t < t0],[U/t0*undefined, t = t0],[0, t0 < t])](images_ft/ft103.gif)
| > | laplace(subs(t0=1,U=2,troj),t,p); |
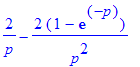
| > |
| > |
| > |
Laplaceova transformace
| > | 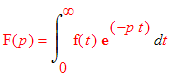
|
Zpětná Laplaceova transformace
| > | 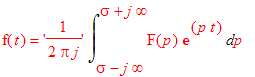
|
| > |
Úloha 2.1.1
| > | ex:=U*exp(-a*t); |
![]()
| > | plot(subs(U=1,a=3,ex)*Heaviside(t),t=-1..2,thickness=2); |
![[Maple Plot]](images_ft/ft108.gif)
| > | int(ex*exp(-I*omega*t),t=-infinity..infinity) assuming a>0; |
![]()
| > | int(ex*exp(-I*omega*t),t=0..infinity) assuming a>0; |
![]()
| > | int(ex*Heaviside(t)*exp(-I*omega*t),t=-infinity..infinity) assuming a>0; |
![]()
Pozor, jednotkový skok je nutný.
| > | fourier(ex,t,omega) assuming a>0; |
| > | fourier(ex*Heaviside(t),t,omega) assuming a>0; |
![]()
![]()
| > | ex2:=U*exp(-a*(t-t0)); |
![]()
| > | plot(subs(U=1,a=3,t0=0.2,ex2*Heaviside(t-t0)),t=-1..2,thickness=2); |
![[Maple Plot]](images_ft/ft115.gif)
| > | fourier(ex2*Heaviside(t-t0),t,omega) assuming a>0, t0>0; |
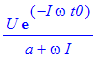
| > |
Úloha 2.1.3
Máme určit frekvenční přenos obvodu (do kmitočtu
![]() , kde už je přenos obvod u téměř nulový. Obvod máme vybudit pulzem a kmitočtový přenos pak určit z jeho odezvy. Jak úzký pulz je třeba pro vybuzení obvodu?
, kde už je přenos obvod u téměř nulový. Obvod máme vybudit pulzem a kmitočtový přenos pak určit z jeho odezvy. Jak úzký pulz je třeba pro vybuzení obvodu?
Spektrum pulzu.
| > | F_rec; |
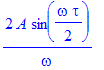
Lépe je to vidět z tohoto vztahu
![]() . Dosaďme
. Dosaďme
![]() , tj.
, tj.
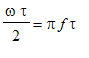 a označme součin
a označme součin
![]() . Pak vyneseme, jak se zmenšuje spektrum v závislosti na tomto součinu (relativně vůči ploše
. Pak vyneseme, jak se zmenšuje spektrum v závislosti na tomto součinu (relativně vůči ploše
![]() ).
).
| > | plot(sin(Pi*x)/(Pi*x),x=0..1); |
![[Maple Plot]](images_ft/ft124.gif)
Jestliže zvolíme
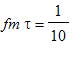 , pak spektrum takového pulzu vykazuje pro tento kmitočet
, pak spektrum takového pulzu vykazuje pro tento kmitočet
![]() pokles cca o 2%, což je možné tolerovat.
pokles cca o 2%, což je možné tolerovat.
| > | evalf(subs(x=0.1,sin(Pi*x)/(Pi*x))); |
![]()
Prakticky např. pro
![]() kHz vychází
kHz vychází
![]() s.
s.
| > | solve(100e3*tau=0.1); |
![]()
| > |
Úloha 2.1.4
| > | S:=1/1000; |
| > | u2:=1/2*exp(-1000*t)*Heaviside(t); |
![]()
![]()
| > | U1:=fourier(Dirac(t)*S,t,omega); |
| > | U2:=fourier(u2,t,omega); |
![]()
![]()
| > | P:=U2/U1; |
![]()
| > | evalf(numer(P)/1000,1)/evalf((denom(P)/1000),1); |
![]()
| > |
Příklad 2.1.4
| > | u1:=2*exp(-2000*t)*Heaviside(t); |
| > | u2:=(8*exp(-2000*t)-6*exp(-3000*t)-2*exp(-1000*t))*Heaviside(t); |
![]()
![]()
| > | U1:=fourier(u1,t,omega); |
| > | U2:=fourier(u2,t,omega); |
| > | P:=U2/U1; |
![]()
![]()
![]()
| > |
Výpočty pomocí Laplaceovy transformace
Laplaceova transformace Diracova pulzu.
| > | laplace(Dirac(t),t,p); |
![]()
Laplaceova transformace jednotkového skoku.
| > | laplace(Heaviside(t),t,p); |
![]()
Příkaz "laplace" evidentně ignoruje funkční hodnoty pro
![]() (integruje se od 0).
(integruje se od 0).
| > | laplace(1,t,p); |
![]()
Následují výpočty některých výše uvedených příkladů pomocí Laplaceovy transformace.
| > | laplace(U*exp(-a*t),t,p); |
![]()
Je nutné vynásobit jednotkovým skokem.
| > | laplace(U*exp(-a*(t-t0)),t,p); |
| > | laplace(U*exp(-a*(t-t0))*Heaviside(t-t0),t,p) assuming t0>0; |
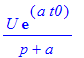
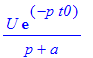
| > | invlaplace(%,p,t) assuming t0>0; |
![]()
| > | u1:=2*exp(-2000*t)*Heaviside(t); |
| > | u2:=(8*exp(-2000*t)-6*exp(-3000*t)-2*exp(-1000*t))*Heaviside(t); |
![]()
![]()
| > | U1:=laplace(u1,t,p); |
| > | U2:=laplace(u2,t,p); |
| > | P:=U2/U1; |
![]()
![]()
![]()
Předpokládá se, že funkce "začíná" v nule.
| > | invlaplace(U2,p,t); |
![]()
| > |