Řady - aproximace funkcí
Hlavní cílem této části je ukázat možnosti aproximace funkcí pomocí řad. Základním příkazem je funkce series , která ve většině případů povede na Taylorovu nebo Laurentovu řadu.
> ?series
>
series(sin(tan(x)),x=0,10);
convert(%,ratpoly);
![]()
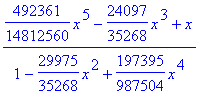
> series(x^x,x=0,5);
> series(x^x,x=1,5);
![]()
![]()
>
Int(ln(1+s*t)^2/(1+t^2),t=0..infinity);
series(%,s=0,5);
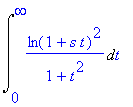
![]()
P
odobně lze řešit i diferenciální rovnice, jak bylo ukázáno výše.
Pro aproximace funkcí slouží zejména knihovna
numapprox,
jejíž některé říkazy si nyní ukážeme na příkladě aproximace funkce
![]() .
.
> restart;
> with(numapprox);
![]()
Apoximace racionální funkcí (Padé).
> pp:=pade(exp(x),x,[3,2]); # racionální funkce 3.(čitatel) a 2.(jmenovatel) řádu
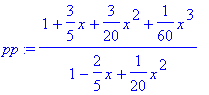
>
plot(exp(x)-pp,x=-2..2); # závislost chyby aproximace na x
maximize(evalf(exp(x)-pp),x,-2..2); # nalezení maximální chyby v uvažovaném oboru hodnot x
![[Maple Plot]](images/MAPLE_IN367.gif)
Error, (in maximize) unexpected options: -2 .. 2
Tento postup je nyní aplikován na jiné druhy aproximací, proto ho již nebudeme komentovat.
Aproximace Čebyševovým polynomem..
>
numapprox[chebyshev](exp(x),x);
pp1:=eval(subs(T=orthopoly[T],%));
![]()
![]()
![]()
![]()
![]()
>
plot(exp(x)-pp1,x=-2..2);
maximize(evalf(exp(x)-pp1),x,-2..2);
![[Maple Plot]](images/MAPLE_IN373.gif)
Error, (in maximize) unexpected options: -2 .. 2
Čebyševova (Padéova) aproximace racionální funkcí.
> Digits:=5:
>
chebpade(exp(x),x=-2..2,[3,2]);
pp2:=eval(subs(T=orthopoly[T],%));
pp3:=confracform(pp2,x);
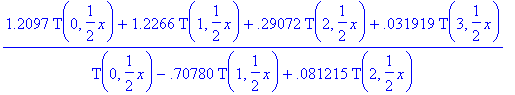
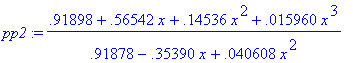
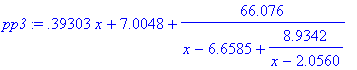
>
plot(exp(x)-pp3,x=-2..2);
maximize(evalf(exp(x)-pp3),x,-2..2);
![[Maple Plot]](images/MAPLE_IN377.gif)
Error, (in maximize) unexpected options: -2 .. 2
Izoextremální aroximace.
>
mn:=minimax(exp(x),x=-2..2,[3,2],1,'err_max');
err_max;
Error, (in numapprox/remez) error curve fails to oscillate sufficiently; try different degrees
![]()
>
plot(exp(x)-mn,x=-2..2);
maximize(evalf(exp(x)-mn),x,-2..2);
Plotting error, empty plot
Error, (in maximize) unexpected options: -2 .. 2
V MAPLE je pro tuto problematiku vytvořen ještě další soubor příkazů v knihovně powerseries . Ten již necháme zvídavým čtenářům k samostatnému studiu.
Do této kapitoly by bylo možné zahrnout i prokládání bodů křivkou, což je úkol statistické matematiky. Tento a další úlohy, spadající do této oblasti, budou ukázány v kapitole Grafika .