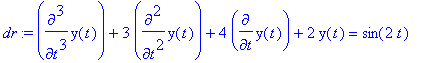
Diferenciální rovnice

Diferenciální rovnice jsou z rozsáhlých kapitol matematiky. Jejich řešení lze, podobně jako u integrálů, rozdělit na analitické a numerické a v obou případech ho lze uskutečnit pomocí příkazu dsolve .

> restart;

> dr:=diff(y(t),t,t,t)+3*diff(y(t),t,t)+4*diff(y(t),t)+2*y(t)=sin(2*t);

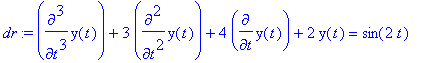
> dsolve(dr,y(t));

> combine(rhs(%));

Výsledek lze jednoduše zkontrolovat omocí příkazu odetest .

> odetest(%%,dr);

Abychom dostali výsledek bez neurčených konstant, je nutné při zadávání rovnice uvést i počáteční podmínky.

> vysl:=combine(dsolve({dr,y(0)=2,D(y)(0)=0,(D@@2)(y)(0)=0},y(t)));

> plot(rhs(vysl),t=0..20);

Lze si určit i metodu řešení. V následujícím příkladě, obdržíme stejný výsledek v mírně odlišném tvaru (lze přímo vyčíst vliv počátečních podmínek) .

> dsolve(dr,y(t),method=laplace);

Toto nebyl náročný příklad (lineární diferenciální rovnice s konstantními koeficienty). V složitých případech, kdy neze najít analitické řešení může ještě pomoci paroximace pomocí Taylorovy řady nebo jiné možné aproximace ( powerseries ). Dále jen numerická řešení, dsolve,numeric .

> dr1:=diff(y(t),t,t)=-sin(y(t));

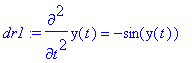
> dsolve(dr1,y(t)); # nenajde analytické řešení

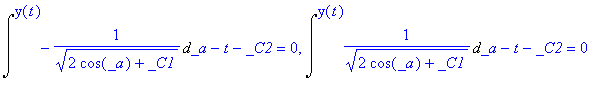
> r6:=dsolve({dr1,y(0)=0,D(y)(0)=1},y(t), type=series);

> y6:=t->convert(rhs(r6),polynom):
y6(t); # aproximace řešení polymomem pátého řádu

> Order:=15;
r15:=dsolve({dr1,y(0)=0,D(y)(0)=1},y(t), type=series);
y15:=t->convert(rhs(r15),polynom):
y15(t); # aproximace řešení polymomem třináctého řádu

> Yn:=dsolve({dr1,y(0)=0,D(y)(0)=1},y(t),type=numeric); # numerické řešení

Numerické řešení je pro konkrétní hodnotu nezáviveproměnné tvaru seznamu, kde první položka udává zmíněnou velikost nezávisle proměnné, druhá a třetí položka numerickou hodnotu výsledné proměnné (řešení) a její derivace v daném bodě.

> Yn(1);

> Y:=t->rhs(op(2,Yn(t)));

> Y(2); # hodnota řešení v bodě t=2

> Yp:=plot(Y,0..2.5): y6p:=plot(y6(t),t=0..2.5,color=blue): y15p:=plot(y15(t),t=0..2.5,color=green):
with(plots):display(Yp,y6p,y15p); # srovnání jednotlivých řešení
plot(Y,0..10); # numerické řešení v širším oboru nezávisle proměnné

Warning, the name changecoords has been redefined

Jak je vidět z obrázku, metodu aproximace řadou lze použít pouze pro omezený rozsah hodnot nezávislé proměnné a ani vyšší řád aproximace tento rozsah významně nezvýší.

Při řešení diferenciálních rovnic lze uplatnit mnoho metod řešení, které se zadavájí v argumentu příkazu dsolve . Jejich pouhý výčet přesahuje rámec tohoto dokumrntu, proto odkážeme zájemce na uvedenou literaturu, případně help.

Samozřejme, že lze řešit i soustavy diferenciálních rovnic, podobně jako tomu je se soustavami algebraických rovnic. Zápis je velmi podobný a lze ho najít i v helpu dsolve,system , proto se dále tímto problémem zabývat nebudeme.