Integrální transformace

MAPLE má zabudovaný výpočet pro Fourierovu (exponenciální, sinovu, cosinovu) transformaci, Laplaceovu, Hilbertovu, Hankelovu a Mellinovu. My se budeme zabývat pouze prvními dvěma, navíc pak numerickou FFT a jejich transformace inverzní.

> restart; # raději uklidíme

> with(inttrans); # nejdříve je nutné načíst příslušnou knihovnu

> f:=Heaviside(t); # f je jednotkový skok

> plot(f, t=-1..1);

> convert(fourier(g(t),t,s),int); #takto lze zobrazit definice transformací
convert(invfourier(g(t),t,s),int);

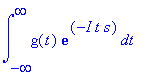
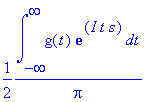
> fourier(f,t,omega);
simplify(invfourier(%,omega,t));

> laplace(f,t,p); # to by nemělo činit potíže

> laplace(sin(x)*cos(x),x,p); # o něco složitější příklad
expand(simplify(invlaplace(%,p,x)));

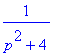
> laplace(exp(-lambda*t)*sin(omega*t+phi),t,p); # a ještě jeden
combine(invlaplace(%,p,t));
Jak je zřejmé, slovníky Laplaceovy transformace se stávají přežitkem.

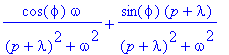
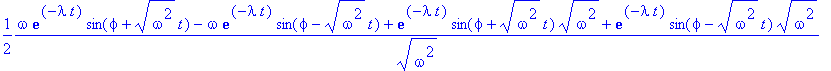
FFT je v mnoha odvětvích velmi používaný nástroj, proto ji budeme věnovat trochu více pozornosti.

> ### WARNING: persistent store makes one-argument readlib obsolete
readlib(FFT); # musíme načíst potřebnou knihovnu

> x:=array([-1,-1,-1,-1,1,1,1,1]): # definice prnvího vstupního vektoru
y:=array([0,0,0,0,0,0,0,0]): # definice druhého (nulového) vstupního vektoru
FFT(3,x,y): # volání FFT - první parametr udává její délku, v našem případě 2^3=8
print(x); # výstup z FFT se zapíše do vstupních vektorů, v našem případě reálná složka výstupu do vektoru x, imaginární část do vektotu y

> iFFT(3,x,y):
print(x); # kontrola zpětnou transformací

Použitelnější bude další, již více reálný, příklad.

> N:=8:f:=2:
vzorky_re:=array([evalf(seq(sin(x*2*Pi*f/2^N),x=1..2^N))]):
vzorky_im:=array([seq(0,x=1..2^N)]):

> pl:=[seq([i*2*Pi*f/2^N,vzorky_re[i]],i=1..2^N)]:
plot(pl,style=POINT);

> FFT(N,vzorky_re,vzorky_im):

> vystup:=[seq(vzorky_re[i]+I*vzorky_im[i],i=1..2^N)]:
vystup_abs:=map(2/2^N*abs, vystup): # je nutno násobit činitelem 2/2^N, abychom dostali správný výsledek (násobící koeficient závisí na dané implementaci FFT).

> pl:=[seq([i-1,vystup_abs[i]],i=1..2^N)]:
plot(pl);

Tento příklad lze dále modifikovat (lze přidávat další harmonické, ...), což ponecháme na čtenáři.

Použití FFT (iFFT) při rekonstrukci zašuměného signálu - lze vynechat