Dvojitý T-článek

[Maple Bitmap]  

Zadání obvodu podle výše uvedeného obrázku.

>    T2:="dvojity T clanek

>    V 1 0 1

>    C1 1 2 C

>    C2 2 3 C*a

>    R3 2 0 R/b

>    R1 1 4 R

>    R2 4 3 R/a

>    C3 4 0 C*b

>    .end":

>    res_T2:=syrup(T2, ac); 

parsedeck:   Analyzing SPICE deck "dvojity T clanek" (ignoring this line)

res_T2 := {v[1] = 1, v[4] = (b+s*C*R*a+s*C*R)/(s^2*C^2*R^2*b+s*C*R*a+s*C*R*a*b+s*C*R+s*C*R*b^2+b), v[3] = (s^2*C^2*R^2*b+s*C*R*a+s*C*R+b-s*C*R*b)/(s^2*C^2*R^2*b+s*C*R*a+s*C*R*a*b+s*C*R+s*C*R*b^2+b), v[...
res_T2 := {v[1] = 1, v[4] = (b+s*C*R*a+s*C*R)/(s^2*C^2*R^2*b+s*C*R*a+s*C*R*a*b+s*C*R+s*C*R*b^2+b), v[3] = (s^2*C^2*R^2*b+s*C*R*a+s*C*R+b-s*C*R*b)/(s^2*C^2*R^2*b+s*C*R*a+s*C*R*a*b+s*C*R+s*C*R*b^2+b), v[...

Obecný výraz pro přenos.

>    P_T2:=subs(res_T2,v[3]);

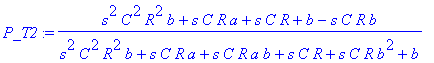
P_T2 := (s^2*C^2*R^2*b+s*C*R*a+s*C*R+b-s*C*R*b)/(s^2*C^2*R^2*b+s*C*R*a+s*C*R*a*b+s*C*R+s*C*R*b^2+b)

Výpočet kmitočtu omega[0] .

>    solve(evalc(Im(subs(s=I*omega,P_T2))),omega);

0, -1/(C*R), 1/(C*R)

>    om_T2:=%[3];

om_T2 := 1/(C*R)

Přenos pro omega[0] = 1 .

>    P_T21:=collect(algsubs(C*R=1,subs(res_T2,v[3])),s);

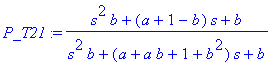
P_T21 := (s^2*b+(a+1-b)*s+b)/(s^2*b+(a+a*b+1+b^2)*s+b)

Přenos pro omega = omega[0] .

>    simplify(subs(s=I/C/R,P_T2));

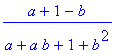
(a+1-b)/(a+a*b+1+b^2)

Strmost fázové charakteristiky pro relativní kmitočet v bodě omega = omega[0] .

>    phi_P_T2:=evalc(argument(subs(s=I*omega,P_T2))):

>    SR_phi_T2:=simplify(om_T2*subs(omega=om_T2,diff(phi_P_T2,omega)));

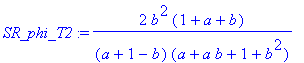
SR_phi_T2 := 2*b^2*(1+a+b)/(a+1-b)/(a+a*b+1+b^2)

Jak bude vidět dále, modul přenosu vykazuje pro omega = omega[0]   opět minimum, článek je tedy opět určen pro větev záporné zpětné vazby. Velikost konstant a  a b  určíme opět tak, aby strmost fázové chrakteristiky byla pro omega = omega[0]  co největší. Ze vztahu SR_phi_T2  je patrné, že jeho velikost můžeme zásadně ovlivnit částí a+1-b , jehož hodnotu lze nastavit velmi malou. Pro použití v ZZV by pak neměl článek otáčet fázi a tudíž by mělo být dodrženo b < a+1 .

Výpočet modulu a fáze přenosu omega[0] = 1 .

>    abs_P_T2:=evalc(abs(subs(s=I*omega,P_T21))):

>    phi_P_T2:=evalc(argument(subs(s=I*omega,P_T21))):

Následuje vykreslení kmitočtových charakteristik pro dvě různé volby hodnot koeficienů a  a b . Dále pak vyčíslení velikosti modulu a strmosti fázové charakteristiky (v radiánech i ve stupních) pro omega = omega[0]  (pro obě hodnoty volby koeficientů).

>    plots[semilogplot]([subs(a=1,b=1,abs_P_T2),subs(a=1,b=1.9,abs_P_T2),subs(a=1,b=2.1,abs_P_T2)],omega=0.1..10,color=[red,blue,green],legend=["a=b=1","a=1, b=1.9","a=1, b=2.1"],thickness=2);

>    plots[semilogplot]([subs(a=1,b=1,phi_P_T2),subs(a=1,b=1.9,phi_P_T2),subs(a=1,b=2.1,phi_P_T2)],omega=0.1..10,color=[red,blue,green],legend=["a=b=1","a=1, b=1.9","a=1, b=2.1"],thickness=2);

>    simplify([subs(a=1,b=1,omega=1,abs_P_T2),subs(a=1,b=19/10,omega=1,abs_P_T2),subs(a=1,b=21/10,omega=1,abs_P_T2)]);

>    evalf([subs(a=1,b=1,SR_phi_T2),subs(a=1,b=1.9,SR_phi_T2),subs(a=1,b=2.1,SR_phi_T2)]);

>    evalf(180/Pi*[subs(a=1,b=1,SR_phi_T2),subs(a=1,b=1.9,SR_phi_T2),subs(a=1,b=2.1,SR_phi_T2)]);

[Maple Plot]

[Maple Plot]

[1/4, 10/751, 10/851]

[1.500000000, 37.49400798, -42.49353702]

[85.94366926, 2148.248414, -2434.700327]

Z grafů je evidentní, že volba konstant a  a b  má zásadní vliv na přenosové vlastnosti článku. Pro relativní změnu Delta*omega[0]/omega[0] = 1 % bude tedy pro a = .77, b = 10  strmost Delta*SR_phi_T = 1.5  stupňů, což je osmkrát lepší hodota oproti volbě a = 1, b = 1 .  

Z grafů je evidentní, že volba konstant a  a b  má zásadní vliv na přenosové vlastnosti článku. Pro volbu a = 1, b = 1.9  (což je ještě stabilní volba "daleko" od relace a+1 = b ) je pro strmost fázové charakteristiky 37 stupňů. Pro změnu Delta*omega[0] = 1 % bude tedy pro danou volbu konstant a  a b  strmost Delta*SR_phi_T2 = 21  stupňů, což je 25 krát lepší hodota oproti volbě a = 1, b = 1 !    

>   

Závislosti pro a=b=0.5, 1 a 2

>   

>    P_T21;

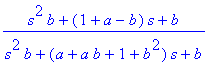
(s^2*b+(1+a-b)*s+b)/(s^2*b+(a+a*b+1+b^2)*s+b)

Přenos má komplexně sdruženou nulu, která je pro 1+a < b  dokonce v pravé polorovině a dále póly, které jsou zde uvedeny, pro různé hodnoty koeficienty b  a pro a = 1 .

>    n1:=solve(subs(a=1.,b=1,numer(P_T21)));

>    n2:=solve(subs(a=1,b=1.9,numer(P_T21)));

>    n3:=solve(subs(a=1,b=2.1,numer(P_T21)));

>    p1:=solve(subs(a=1.,b=1,denom(P_T21)));

>    p2:=solve(subs(a=1,b=1.9,denom(P_T21)));

>    p3:=solve(subs(a=1,b=2.1,denom(P_T21)));

n1 := -.5000000000+.8660254038*I, -.5000000000-.8660254038*I

n2 := -.2631578947e-1+.9996536796*I, -.2631578947e-1-.9996536796*I

n3 := .2380952381e-1+.9997165131*I, .2380952381e-1-.9997165131*I

p1 := -.2679491924, -3.732050808

p2 := -.2716679960, -3.680963583

p3 := -.2639623849, -3.788418568

Vykreslení polohy pólů a nul pro výše uvedené volby koeficientů.

>    n1pl:=plots[complexplot]([n1],style=point,symbol=CIRCLE,symbolsize=20,color=red,legend="a=1, b=1"):

>    n2pl:=plots[complexplot]([n2],style=point,symbol=CIRCLE,symbolsize=20,color=blue,legend="a=1, b=1.9"):

>    n3pl:=plots[complexplot]([n3],style=point,symbol=CIRCLE,symbolsize=20,color=green,legend="a=1, b=2.1"):

>    p1pl:=plots[complexplot]([p1],style=point,symbol=CROSS,symbolsize=20,color=red,legend="a=1, b=1"):

>    p2pl:=plots[complexplot]([p2],style=point,symbol=CROSS,symbolsize=20,color=blue,legend="a=1, b=1.9"):

>    p3pl:=plots[complexplot]([p3],style=point,symbol=CROSS,symbolsize=20,color=green,legend="a=1, b=2.1"):

>    plots[display](p1pl,p2pl,p3pl);

>    plots[display](n1pl,n2pl,n3pl);

[Maple Plot]

[Maple Plot]