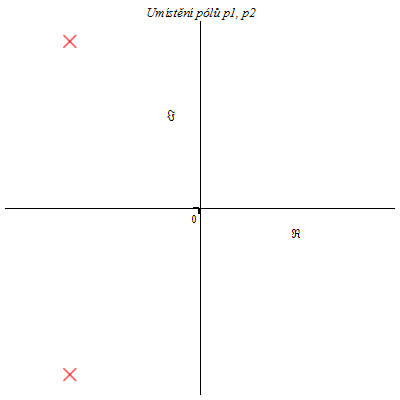
Komlexně sdružená dvojice pólů se zápornou reálnou částí
Např. pro ![]() ,
, ![]() a
a ![]() dostaneme
dostaneme
| > | Pf:=abs(subs({K=1000^2,p1=-200+I*980,p2=-200-I*980,p=sigma+I*omega},P)); |
| (3.1.1) |
| > | complexplot([-200+I*980,-200-I*980],Re=-300..300,Im=-1100..1100,style=point,symbol=cross,tickmarks=[1,1],title=`Umístění pólů p1, p2`,labelfont=[HELVETICA],axesfont=[HELVETICA,8],symbolsize=25,symbol=diagonalcross); |
 |
Přenos tohoto typu vykazyje například takovýto jednoduchý rezonanční RLC obvod.
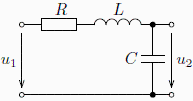
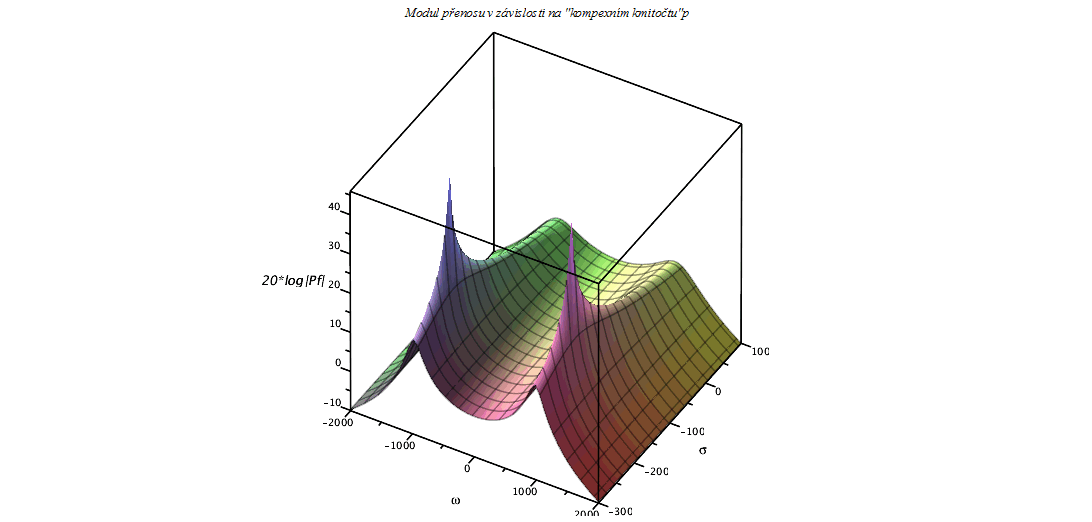
V následujících grafech je vynášen přenos vždy v dB, abychom dosáhli "větší dynamiky" na ose přenosu. Z těchto a předcházejících grafů je také zřejmé, proč pouze komlexně združené kořeny mohou vyvolat tzv. "překmit" na modulové charakteristice. Tím, že má pól nenulovou imaginární část nastává maximum ![]() na jiném kmitočtu než na
na jiném kmitočtu než na ![]() . (nastává pro
. (nastává pro ![]() a
a ![]() ).
).
| > | plot3d(20*log10(Pf),omega=-2000..2000,sigma=-300..100,style=patch,axes=box,orientation=[-60,50],numpoints=2000,labels=[`omega`,`sigma`,`20*log|Pf|`],numpoints=3000,title=`Modul přenosu v závislosti na "kompexním kmitočtu"p`,labelfont=[HELVETICA],axesfont=[HELVETICA,8]);
plot3d(20*log10(Pf),omega=1..3000,sigma=-10..10,style=patch,axes=box,orientation=[-60,50],title=`Modul přenosu v závislosti na "kompexním kmitočtu" p`,labelfont=[HELVETICA],axesfont=[HELVETICA,8]); |
 |
|
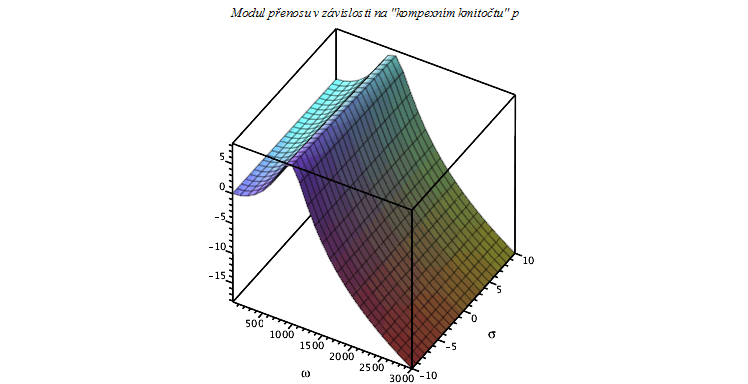 |
Je pochopitelné, že pro reálný kladný kmitočet nenastane maximum přenosu, ale může nastat poze "překmit" modulové charakteristiky tak, jak je vidět na tomto obrázku. Dále už budeme vykreslovat grafy pouze pro kladné ![]() .
.
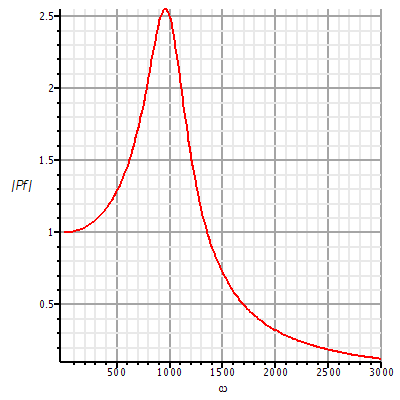
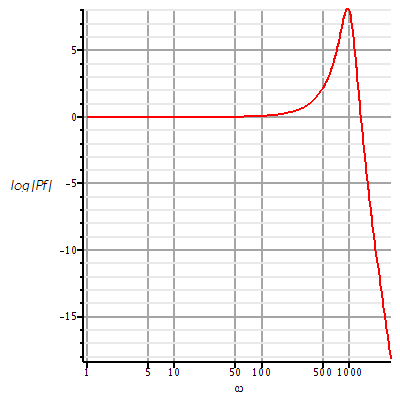
Následuje průběh modulové charakteristiky přenosu vykreslený v lineárním a logaritmickém měřítku.
| > | display(matrix(1,2,[plot(subs(sigma=0,Pf),omega=1..3000,labels=[omega,`|Pf|`],axes=FRAME,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2,gridlines=true),semilogplot(20*log10(subs(sigma=0,Pf)),omega=1..3000,labels=[omega,`log|Pf|`],axes=FRAME,labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2,gridlines=true)],array)); |
|
Časovou odezvu tohoto systému na Diracův impulz ukážeme v závěru celé této seckce. Tuto otázku potom vyřešíme obecněji pro všechny typy lineárních sysrémů, tedy i nestabilními, kterými se pro úplnost budeme zabývat v následujícím výkladu.