Komplexně sdružená dvojice pólů a nula v nule (nulovém kmitočtu) - pásmová propust (PP)
Přenosová funkce je ve tvaru
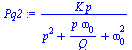 |
(7.3.1) |
Např. pro 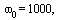
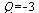 a
a ![K = `/`(`*`(omega[0]), `*`(Q))](images_pl/pol_nul_386.gif) dostaneme následující kmotičtové charakteristiky
dostaneme následující kmotičtové charakteristiky
| > |
Pf:=subs({K=1000/4,omega[0]=1000,Q=4,p=I*omega},Pq2):
semilogplot(20*log10(abs(Pf)),omega=100..10000,y=-32..0,title=`Modulová charakteristika s logaritmickým měřítkem kmitočtu [dB]`,labels=[omega,`log|Pf|`],axes=FRAME,labelfont=[HELVETICA], axesfont=[HELVETICA,8],thickness=2,gridlines=true);
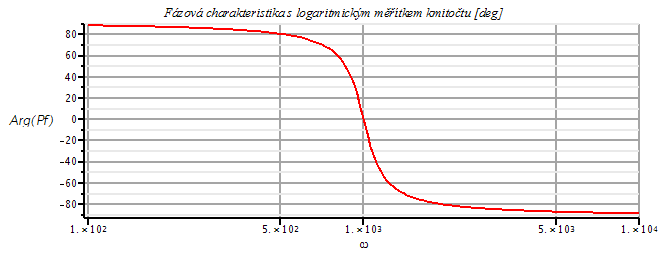
semilogplot(180/Pi*argument(Pf),omega=100..10000,y=-90..90,title=`Fázová charakteristika s logaritmickým měřítkem kmitočtu [deg]`,labels=[omega,`Arg(Pf)`], axes=FRAME,labelfont=[HELVETICA], axesfont=[HELVETICA,8],thickness=2,gridlines=true);
|
Volba ![K = `/`(`*`(omega[0]), `*`(Q))](images_pl/pol_nul_389.gif) byla určena tak, aby zisk v propustném pásmu
byla určena tak, aby zisk v propustném pásmu ![H[0]](images_pl/pol_nul_390.gif) byl právě 1, tj. 0dB, jelikož
byl právě 1, tj. 0dB, jelikož
| > |
'Pq2(omega[0])=H[B]'=simplify(subs(p=I*omega[0],Pq2)); |
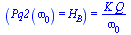 |
(7.3.2) |
Fáze přenosu je pro tento zlomový kmitočet (![omega = omega[0]](images_pl/pol_nul_392.gif) ) evidentmě nulová a maximum modulové charakteristiky nastává také pří tomto kmitočtu.
) evidentmě nulová a maximum modulové charakteristiky nastává také pří tomto kmitočtu.
| > |
solve(diff(evalc(abs(subs(p=I*omega,Pq2))),omega),omega);
evalf(subs({K=1000/4,omega[0]=1000,Q=4},[%])); |
Nyní najděme kmitočet poklesu modulu přenosu o 3dB oproti maximu:
| > |
om12:=solve(evalc(abs(subs(K=omega[0]/Q,p=I*omega,Pq2)))=1/sqrt(2),omega);
evalf(subs({K=1000/4,omega[0]=1000,Q=4},[%])); |
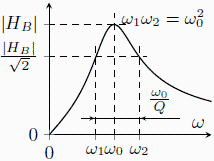
Je zřejmé, že 2. a 4. výsledek je záporný. Uvažujme tedy pouze dva výsledky ![om12[1] = omega[2]](images_pl/pol_nul_400.gif) a
a ![om12[3] = omega[1]](images_pl/pol_nul_401.gif) , které jsou ilustrovány na tomto obrázku a níže je důkaz uvedených skutečností.
, které jsou ilustrovány na tomto obrázku a níže je důkaz uvedených skutečností.
| > |
'omega[2]-omega[1]'=simplify(om12[1]-om12[3]); |
| > |
'omega[1]*omega[2]'=simplify(om12[3]*om12[1]); |
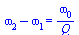 |
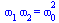 |
(7.3.5) |
Hodnota fáze přenosu pro zlomový kmitočet ![omega[0]](images_pl/pol_nul_405.gif) .
.
| > |
simplify(evalc(argument(subs(p=I*omega[0],Pq2)))) assuming Q>1, K>0, omega[0]>0; |
 |
(7.3.6) |
Časová odezva je následkující
| > |
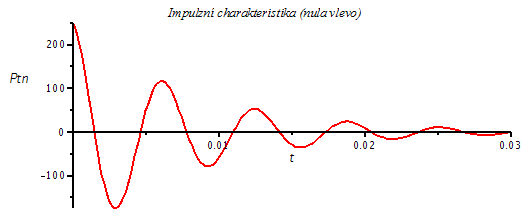
Ptn:=invlaplace(subs({K=1000/4,omega[0]=1000,Q=4},Pq2), p, t);
plot(Ptn,t=0..0.03,title=`Impulzní charakteristika (nula vlevo)`,labels=[t,`Ptn `],labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
Jak bylo odvozeno výše, charakter odezvy je plně určen charakterem pólů přenosu, tj. kmitočet odezvy je dán imaginární částí pólu, zatímco tlumení je dáno jeho reálnou částí.
| > |
'p12'=solve(subs({omega[0]=1000,Q=4},denom(Pq2))); |
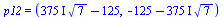 |
(7.3.7) |
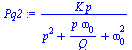
![]()
![]() a
a ![]() dostaneme následující kmotičtové charakteristiky
dostaneme následující kmotičtové charakteristiky 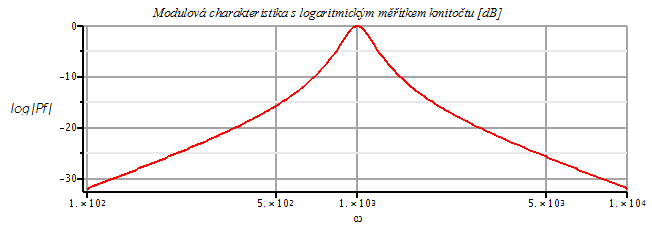
![]() byla určena tak, aby zisk v propustném pásmu
byla určena tak, aby zisk v propustném pásmu ![]() byl právě 1, tj. 0dB, jelikož
byl právě 1, tj. 0dB, jelikož ![]() ) evidentmě nulová a maximum modulové charakteristiky nastává také pří tomto kmitočtu.
) evidentmě nulová a maximum modulové charakteristiky nastává také pří tomto kmitočtu. ![]() a
a ![]() , které jsou ilustrovány na tomto obrázku a níže je důkaz uvedených skutečností.
, které jsou ilustrovány na tomto obrázku a níže je důkaz uvedených skutečností. 
![]() .
.