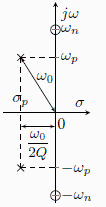
Komplexně sdružená dvojice pólů a komlexně sdružená dvojice nul na imaginární ose s 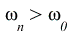 : eliptická dolní propust (DP)
: eliptická dolní propust (DP)
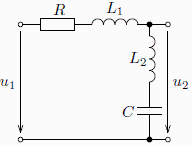
Přenosová funkce je ve tvaru:
| > |
Pqe:=subs({n1=I*omega[n],n2=-I*omega[n]},Pq);
simplify(%); |
 |
 |
(8.1.1) |
Limitní hodnoty modulu přenosu pro DC a velmi vysoký kmitočet jsou následující:
| > |
'Pqe(infinity)'=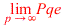 |
 |
(8.1.2) |
| > |
'Pqe(0)'=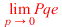 |
![Pqe(0) = `/`(`*`(`^`(omega[n], 2), `*`(K)), `*`(`^`(omega[0], 2)))](images_pol_nul/pol_nul_464.gif) |
(8.1.3) |
Ani jedna z hodnot není nulová (systém má nennulový přenos). Pokud platí  jedná o DP, přičemž rozdíl mezi přenosem v propustném a nepropustném pásmu je dán právě podílem
jedná o DP, přičemž rozdíl mezi přenosem v propustném a nepropustném pásmu je dán právě podílem ![`/`(`*`(`^`(omega[n], 2)), `*`(`^`(omega[0], 2)))](images_pol_nul/pol_nul_466.gif) . Násobná konstanta se obvykle udává ve tvaru
. Násobná konstanta se obvykle udává ve tvaru ![K = `/`(`*`(`^`(omega[0], 2), `*`(H[0])), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_467.gif) . Potom
. Potom ![H[0]](images_pol_nul/pol_nul_468.gif) udává přímo zisk v propustném pásmu.
udává přímo zisk v propustném pásmu.
![`/`(`*`(`^`(omega[n], 2)), `*`(`^`(omega[0], 2)))](images_pol_nul/pol_nul_470.gif) |
(8.1.4) |
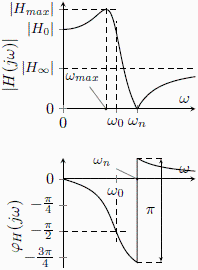
Hodnota převýšení modulové charakteristiky pro zlomový kmitočet ![omega[0]](images_pol_nul/pol_nul_471.gif) je o něco menší než Q a fáze přenosu pro zlomový kmitočet je -π/2.
je o něco menší než Q a fáze přenosu pro zlomový kmitočet je -π/2.
![omega[0]](images_pol_nul/pol_nul_472.gif) |
(8.1.5) |
| > |
`Pqe(omega[0])`=simplify(evalc(abs(subs({p=I*omega[0],K = omega[0]^2*H[0]/omega[n]^2},Pqe)))) assuming Q>0, H[0]>0, omega[0]>0, omega[n]>omega[0];
subs({H[0]=1,omega[0]=1000,omega[n]=5000.,Q=4,p=I*omega},%); |
| > |
'phi__Pqe(omega[0])'=simplify(evalc(argument(subs(p=I*omega[0],Pqe)))) assuming Q>1, K>0, omega[0]>0, omega[n]>omega[0]; |
Minimum modulové charakteristiky nastává při kmitočtu  kde se fáze přenosu mění skokově o
kde se fáze přenosu mění skokově o 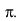 Přenos změní skokově znaménko, jelikož přejdečitatel
Přenos změní skokově znaménko, jelikož přejdečitatel ![`+`(`*`(`^`(p, 2)), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_478.gif) přejde na
přejde na ![`+`(`-`(`*`(`^`(omega, 2))), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_479.gif) , který pro
, který pro ![`<`(omega, omega[n])](images_pol_nul/pol_nul_480.gif) vyjde kladně a
vyjde kladně a ![`>`(omega, omega[n])](images_pol_nul/pol_nul_481.gif)
![omega = omega[n]](images_pol_nul/pol_nul_482.gif)
| > |
subs(p=I*omega[n],Pqe); |
 |
(8.1.7) |
Např. pro 
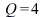 a
a ![H[0] = 1](images_pol_nul/pol_nul_486.gif) (tj.
(tj. ![K = `/`(`*`(`^`(omega[0], 2)), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_487.gif) ), dostaneme následující kmtičtové charakteristiky
), dostaneme následující kmtičtové charakteristiky
| > |
Pf:=subs({K=1000^2/5000^2,omega[0]=1000,omega[n]=5000,Q=4,p=I*omega},Pqe):
semilogplot(20*log10(abs(Pf)),omega=100..100000,title=`Modulová charakteristika s logaritmickým měřítkem kmitočtu`,labels=[omega,typeset(20*log10(abs('Pqe'))," [dB]")],axes=FRAME,labelfont=[HELVETICA], axesfont=[HELVETICA,8],thickness=2,gridlines=true);
semilogplot(180/Pi*argument(Pf),omega=100..100000,title=`Fázová charakteristika s logaritmickým měřítkem kmitočtu`,labels=[omega,typeset(varphi['Pqe']," [°]")], axes=FRAME,labelfont=[HELVETICA], axesfont=[HELVETICA,8],thickness=2,gridlines=true);
|
Mmaximum modulové charakteristiky nastává pří kmitočtu ![omega__max = `+`(`-`(`/`(`*`(sqrt(`*`(`+`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[0], 2)))), `-`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[n], 2))))), `-`(`*`(`^`(omega[0], 2)))), `*`(`+`(`*`(2, `*`(`^`(Q, 2), ...](images_pol_nul/pol_nul_490.gif) a maximum je rovno
a maximum je rovno 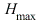 . Vyjádření obou veličin v symbolickém tvaru je již poměrně komplikované.
. Vyjádření obou veličin v symbolickém tvaru je již poměrně komplikované.
| > |
solve(diff(evalc(abs(subs(p=I*omega,Pqe))),omega),omega) assuming Q>1, K>0, omega[0]>0, omega[n]>0;
evalf(subs({K=1000^2/5000^2,omega[0]=1000,omega[n]=5000,Q=4},[%]));
simplify(subs({p=I*(%%[3])},abs(Pqe))) assuming Q>1, K>0, omega[0]>0, omega[n]>omega[0];
evalf(subs({K=1000^2/5000^2,omega[0]=1000,omega[n]=5000,Q=4},[%])); |
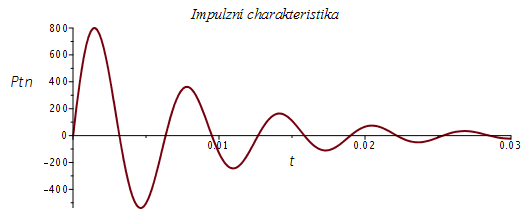
Časová odezva odpovídá výše uvedené neeliptické DP, jelikož nuly neovlivňují její charaktrer.
| > |
Ptn:=invlaplace(subs({K=1000^2/5000^2,omega[0]=1000,omega[n]=5000,Q=4},Pqe), p, t);
plot(Ptn,t=0..0.03,title=`Impulzní charakteristika`,labels=[t,`Ptn `],labelfont=[HELVETICA],axesfont=[HELVETICA,8],thickness=2); |
Kmitočet odezvy je dán imaginární částí pólu, zatímco tlumení je dáno jeho reálnou částí.
| > |
'p12'=solve(subs({omega[0]=1000,Q=4},denom(Pqe))); |
 |
(8.1.9) |
![]() : eliptická dolní propust (DP)
: eliptická dolní propust (DP) 



![Pqe(0) = `/`(`*`(`^`(omega[n], 2), `*`(K)), `*`(`^`(omega[0], 2)))](images_pol_nul/pol_nul_464.gif)
![]() jedná o DP, přičemž rozdíl mezi přenosem v propustném a nepropustném pásmu je dán právě podílem
jedná o DP, přičemž rozdíl mezi přenosem v propustném a nepropustném pásmu je dán právě podílem ![]() . Násobná konstanta se obvykle udává ve tvaru
. Násobná konstanta se obvykle udává ve tvaru ![K = `/`(`*`(`^`(omega[0], 2), `*`(H[0])), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_467.gif) . Potom
. Potom ![]() udává přímo zisk v propustném pásmu.
udává přímo zisk v propustném pásmu. 
![]() je o něco menší než Q a fáze přenosu pro zlomový kmitočet je -π/2.
je o něco menší než Q a fáze přenosu pro zlomový kmitočet je -π/2. 
![]() kde se fáze přenosu mění skokově o
kde se fáze přenosu mění skokově o ![]() Přenos změní skokově znaménko, jelikož přejdečitatel
Přenos změní skokově znaménko, jelikož přejdečitatel ![]() přejde na
přejde na ![]() , který pro
, který pro ![]() vyjde kladně a
vyjde kladně a ![]()
![]()
![]()
![]() a
a ![]() (tj.
(tj. ![K = `/`(`*`(`^`(omega[0], 2)), `*`(`^`(omega[n], 2)))](images_pol_nul/pol_nul_487.gif) ), dostaneme následující kmtičtové charakteristiky
), dostaneme následující kmtičtové charakteristiky 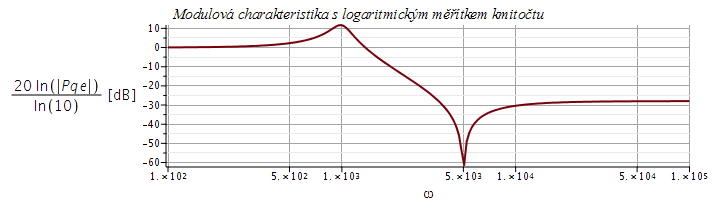
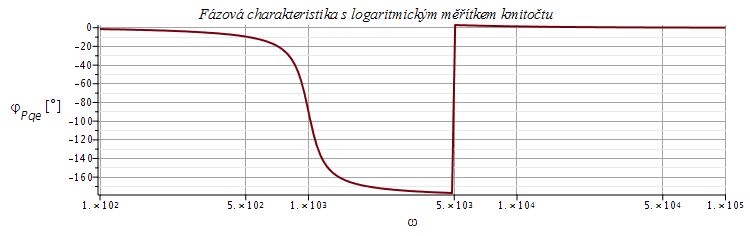
![omega__max = `+`(`-`(`/`(`*`(sqrt(`*`(`+`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[0], 2)))), `-`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[n], 2))))), `-`(`*`(`^`(omega[0], 2)))), `*`(`+`(`*`(2, `*`(`^`(Q, 2), ...](images_pol_nul/pol_nul_490.gif) a maximum je rovno
a maximum je rovno ![]() . Vyjádření obou veličin v symbolickém tvaru je již poměrně komplikované.
. Vyjádření obou veličin v symbolickém tvaru je již poměrně komplikované. ![0, `/`(`*`(`^`(`*`(`+`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[0], 2)))), `-`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[n], 2))))), `-`(`*`(`^`(omega[0], 2)))), `*`(`+`(`*`(2, `*`(`^`(Q, 2), `*`(`^`(omega[0], 2...](images_pol_nul/pol_nul_492.gif)