clanky.html

Wienův článek

Zadání obvodu podle výše uvedeného obrázku.

> wien:="wienuv clanek

> V 1 0 1

> R1 1 2 R*a

> C1 2 3 C/a

> C2 3 0 C

> R2 3 0 R

> .end":

> res_w:=syrup(wien, ac);

parsedeck:   Analyzing SPICE deck "wienuv clanek" (ignoring this line)

$res_w := {v[1] = 1, v[3] = s*C*R/(2*s*C*R*a+a+s^2*C^2*R^2*a+s*C*R), v[2] = (s*C*R+s*C*R*a+a)/(2*s*C*R*a+a+s^2*C^2*R^2*a+s*C*R)}$

Obecný výraz pro přenos.

> P_w:=subs(res_w,v[3]);

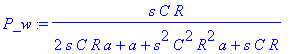
Výpočet kmitočtu .

> solve(evalc(Im(subs(s=I*omega,P_w))),omega);

Přenos pro .

> P_w1:=collect(algsubs(C*R=1,subs(res_w,v[3])),s);

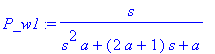
Činitel jakosti.

> Q_w:=1/coeff(denom(P_w1)/a,s,1);

Přenos pro .

> simplify(subs(s=I/C/R,P_w));

Výpočet modulu a fáze přenosu .

> abs_P_w:=evalc(abs(subs(s=I*omega,P_w1))):

> phi_P_w:=evalc(argument(subs(s=I*omega,P_w1))):

Strmost fázové charakteristiky pro . Až na konstantu je strmost shodná s činitelem jakosti.

> SR_phi_w:=simplify(subs(omega=1,diff(phi_P_w,omega)));

Modul přenosu vykazuje pro maximum, z čehož vyplývá, že daný článek je určen pro větev kladné zpětné vazby. Je evidentní, že velikost tohoto přenosu je vždy menší než 1 a je výhodné, aby jeho hodnota nebyla příliš malá, protože zesilovač můstkového oscilátoru by pak pracoval s příliš velkým zesílením. Pro stabilitu kmitočtu je výhodné, aby strmost fázové chrakteristiky byla pro co největší. Zde jdou však tyto požadavky proti sobě. Pro velikost modulu je výhodné, aby koeficient byl malý, pro strmost fáze naopak velký, i když dominantnějši vliv má velikost koeficientu na modul. Častá volba je proto , protože jsou stejné hodnoty R a C.

Následuje vykreslení kmitočtových charakteristik pro tři různé hodnoty koeficienu . Dále pak vyčíslení velikosti modulu a strmosti fázové charakteristiky (v radiánech i ve stupních) pro (pro všechny tři hodnoty koeficientu ).

> plots[semilogplot]([subs(a=0.5,abs_P_w),subs(a=1,abs_P_w),subs(a=2,abs_P_w)],omega=0.1..10,color=[blue,red,green],legend=["a=0.5","a=1","a=2"],thickness=2);

> plots[semilogplot]([subs(a=0.5,phi_P_w),subs(a=1,phi_P_w),subs(a=2,phi_P_w)],omega=0.1..10,color=[blue,red,green],legend=["a=0.5","a=1","a=2"],thickness=2);

> simplify([subs(a=1/2,omega=1,abs_P_w),subs(a=1,omega=1,abs_P_w),subs(a=2,omega=1,abs_P_w)]);

> evalf([subs(a=0.5,SR_phi_w),subs(a=1,SR_phi_w),subs(a=2,SR_phi_w)]);

A teď ve stupních.

> evalf(180/Pi*[subs(a=0.5,SR_phi_w),subs(a=1,SR_phi_w),subs(a=2,SR_phi_w)]);

Strmost (derivace) fáze je vztažena k , resp. poměrnému úhlovému kmitočtu. Pokud budeme chtít znát strmost pro relativní kmitočet, je nutné ji tímto kmitočtem vynásobit . Takovou hodnotu strmosti lze potom jednoduše porovnávat i pro případ, že . Zde je strmost , což znamená, že pro změnu % bude 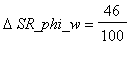stupně. Vzhledem k tomu, že pro tento případ je , je tato hodnota shodná i pro případ relativního kmitočtu, což je dokázáno následujícím výpočtem.

> phi_P_w2:=evalc(argument(subs(s=I*omega,P_w))):

> SR_phi_w2:=simplify(subs(omega=1/R/C,diff(phi_P_w2,omega)));

> SR_phi_w;

> P_w1;

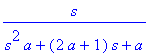
Přenos má jednu nulu v nule a dále póly, které jsou zde uvedeny, pro různé hodnoty koeficientu .

> solve(subs(a=0.5,denom(P_w1)));

> solve(subs(a=1.,denom(P_w1)));

> solve(subs(a=2.,denom(P_w1)));